- #1
skynelson
- 58
- 4
- TL;DR Summary
- Using Fourier series to generate a smooth function, then using Fourier transform to generate a smooth curve of the original coefficient distribution.
Hi, I am interested in understanding the relationships between Fourier series and Fourier transform better. My goal is
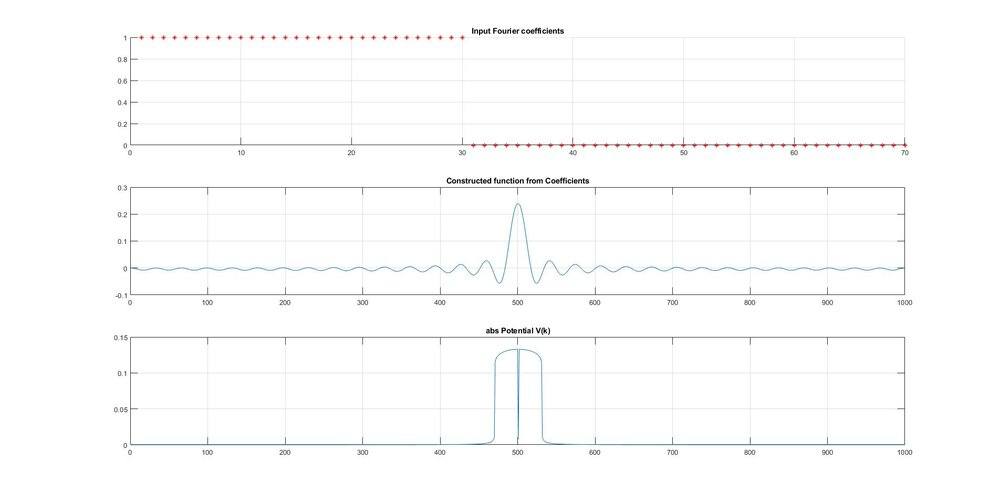
1) Start with a set of ordered numbers representing Fourier coefficients. I chose to create 70 coefficients and set the first 30 to the value 1 and the remaining to zero.
2) Take those coefficients as the amplitudes of plane waves, whose frequency corresponds to the index of the coefficient in the ordered list. Add all these waves together to get a smooth curve (a sinc function).
3) Use the native function fft to try to generate a continuous rect function, corresponding to the sinc function.
This final curve would be the continuous version of the original coefficients, as if they were interpolated.
The first two steps seem successful, but the reproduced rect function is curved on the corners. I suspect this may have something to do with not handling the imaginary portion properly.
Any help getting the code to do what I want would be appreciated! (And any additional wisdom on the goal of this endeavor relating the Fourier series and Fourier transform and interpolation of the Fourier coefficients would be welcome too! Is it a fool's errand?)
1) Start with a set of ordered numbers representing Fourier coefficients. I chose to create 70 coefficients and set the first 30 to the value 1 and the remaining to zero.
2) Take those coefficients as the amplitudes of plane waves, whose frequency corresponds to the index of the coefficient in the ordered list. Add all these waves together to get a smooth curve (a sinc function).
3) Use the native function fft to try to generate a continuous rect function, corresponding to the sinc function.
This final curve would be the continuous version of the original coefficients, as if they were interpolated.
The first two steps seem successful, but the reproduced rect function is curved on the corners. I suspect this may have something to do with not handling the imaginary portion properly.
Any help getting the code to do what I want would be appreciated! (And any additional wisdom on the goal of this endeavor relating the Fourier series and Fourier transform and interpolation of the Fourier coefficients would be welcome too! Is it a fool's errand?)
MATLAB Code:
domain = 1000;
PotentialSize = 70;
X = linspace(1,70,70);
Vbk = zeros(1, PotentialSize);
Vbk(1:30) = 1;
%% PLOT FIGURE
figure('units','normalized','outerposition',[0 0 1 1], 'NumberTitle', 'off', 'Name', 'Scattering');
% Plot the Fourier coefficients
subplot(3,1,1);
scatter( X, Vbk, 'r*');
title('Input Fourier coefficients');
% Construct a continuous time domain function.
Vb1x = FSeries(Vbk,PotentialSize,domain);
Vb1x = Vb1x/norm(Vb1x);
subplot(3,1,2);
plot(fftshift(real(Vb1x)));
title('Constructed function from Coefficients');
% Use native fft function to try to recover the original shape of
%coefficients in frequency domain.
Vb1k = fft(Vb1x);
Vb1k = Vb1k/norm(Vb1k);
subplot(3,1,3);
plot( fftshift(abs(Vb1k)));
title('abs Potential V(k)');
function [o1] = FSeries(Vbk,B,res)
t = linspace(0, 1, res);
result = zeros(size(t));
for b = 1:B
%Turn this into a function of t
%Each Vbk(b) is the b-th coefficient, so it is associated with a cosine
%wave of frequency b.
%Each cosine is layered on to the previous.
result = result + Vbk(b).*cos(2*pi*b*t);
end
o1 = result;
end