- 2,020
- 843
- TL;DR Summary
- I am trying to calculate the time elapsed for the stationary twin solely based on the traveling twins perspective. I've never seen it done this way and I'm screwing something up.
I know, I know, yet another Twin Paradox thread.
(My apologies if this is already on the Forum somewhere. I found a similar discussion but with no answer to my question. I'd appreciate a link if someone has already given an answer to it.)
I'm trying to construct the time elapsed for Stan ("stationary frame") as observed by Moe ("moving frame.") Assume the usual conditions for the paradox. Let Moe leave Earth (A) with a speed of 0.8 (c = 1) and travel out 4 light years (P). Let's also assume that Moe is going to jump on another rocket 4 light years out that is traveling back to Earth at 0.8 (and assume this wouldn't kill him) and returns to Earth (D).
At event B, Stan sends a light beam out to event P to meet Moe. When Moe gets to P and switches direction, he sends a light beam back to Earth at event C.
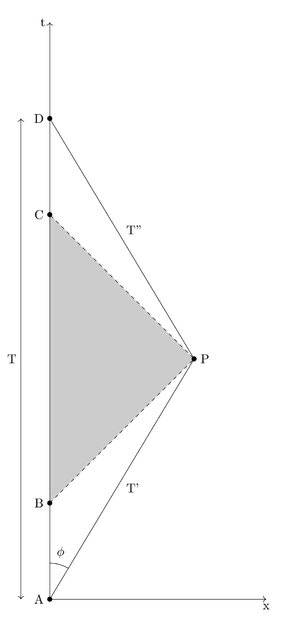
The time elapsed for the whole trip for Stan is ##T = 2 \cdot \dfrac{4}{0.8} = 10## light years. According to Moe, it takes ##T' + T'' = \dfrac{T}{ \gamma } = 6## light years.
That's the usual thing. What I am trying to do is figure out how to calculate this according to Moe. Between the outward and inward trips he sees Stan age 6 light years. Moe sees Stan age 4 light years (almost) instantly when he switches coordinate systems 4 light years out.
The shaded triangle somehow gives the missing 4 years. But is there a way to get that from the triangle? I'm thinking it has something to do with the area of the triangle, and I could theoretically do all sorts of numerology on it to get the answer. But I haven't a clue how to derive it. (And, frankly, just how to find the area of the triangle in Minkowski space would be another question! My Differential Geometry is fairly primitive.)
Thanks!
-Dan
(My apologies if this is already on the Forum somewhere. I found a similar discussion but with no answer to my question. I'd appreciate a link if someone has already given an answer to it.)
I'm trying to construct the time elapsed for Stan ("stationary frame") as observed by Moe ("moving frame.") Assume the usual conditions for the paradox. Let Moe leave Earth (A) with a speed of 0.8 (c = 1) and travel out 4 light years (P). Let's also assume that Moe is going to jump on another rocket 4 light years out that is traveling back to Earth at 0.8 (and assume this wouldn't kill him) and returns to Earth (D).
At event B, Stan sends a light beam out to event P to meet Moe. When Moe gets to P and switches direction, he sends a light beam back to Earth at event C.
The time elapsed for the whole trip for Stan is ##T = 2 \cdot \dfrac{4}{0.8} = 10## light years. According to Moe, it takes ##T' + T'' = \dfrac{T}{ \gamma } = 6## light years.
That's the usual thing. What I am trying to do is figure out how to calculate this according to Moe. Between the outward and inward trips he sees Stan age 6 light years. Moe sees Stan age 4 light years (almost) instantly when he switches coordinate systems 4 light years out.
The shaded triangle somehow gives the missing 4 years. But is there a way to get that from the triangle? I'm thinking it has something to do with the area of the triangle, and I could theoretically do all sorts of numerology on it to get the answer. But I haven't a clue how to derive it. (And, frankly, just how to find the area of the triangle in Minkowski space would be another question! My Differential Geometry is fairly primitive.)
Thanks!
-Dan