D.S.Beyer
- 50
- 2
- TL;DR Summary
- What is the result of the Twin Paradox if the round trip of one twin is entirely on a geodesic?
~ Shower Thoughts ~
Twin A is in a spaceship, Twin B is in a spaceship. Both in 'deep space'.
B follows a highly elliptical geodesic which goes around a planet (or black hole) with strong gravity, very far away.
When they meet again, who is younger and why?
I genuinely don't know what this answer will be.
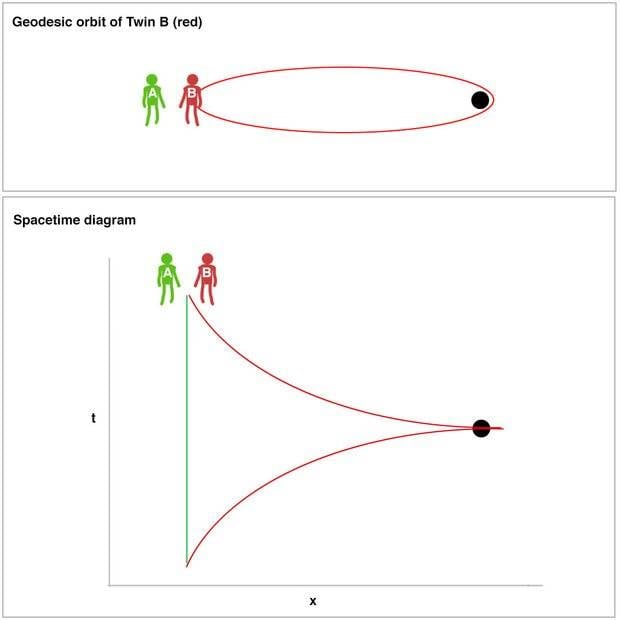
( In an ideal case A stays in Flat Minkowski Spacetime during B's trip. However, A will need to accelerate a little bit away from the distant planet to maintain position. Does this small bit of acceleration may make the difference in the end..? dunno)
I'm going through Eigenchris's youtube videos, and he has an amazing explanation of the Twin Paradox, essentially saying the solution is "The reversed triangle inequality (assuming timeline vectors). In which geodesics have the longest proper time, and non-geodesics have shorter proper time."
That made sense to me in SR terms, so I thought I'd see if I could convolute it with some GR curvature. Since Twin B follows geodesics, and A must slightly accelerate... is A younger? Or is B effected by gravitational time dilation as it goes around the planet and thus B is younger?
Very curious. Thoughts?
Twin A is in a spaceship, Twin B is in a spaceship. Both in 'deep space'.
B follows a highly elliptical geodesic which goes around a planet (or black hole) with strong gravity, very far away.
When they meet again, who is younger and why?
I genuinely don't know what this answer will be.
( In an ideal case A stays in Flat Minkowski Spacetime during B's trip. However, A will need to accelerate a little bit away from the distant planet to maintain position. Does this small bit of acceleration may make the difference in the end..? dunno)
I'm going through Eigenchris's youtube videos, and he has an amazing explanation of the Twin Paradox, essentially saying the solution is "The reversed triangle inequality (assuming timeline vectors). In which geodesics have the longest proper time, and non-geodesics have shorter proper time."
That made sense to me in SR terms, so I thought I'd see if I could convolute it with some GR curvature. Since Twin B follows geodesics, and A must slightly accelerate... is A younger? Or is B effected by gravitational time dilation as it goes around the planet and thus B is younger?
Very curious. Thoughts?