LikenTs
- 24
- 3
- TL;DR Summary
- Twin paradox, special relativity, general relativity, computerized clock in ship showing time on earth.
Conventional Twin Paradox. A ship with speed v = 0.8c makes a round trip from Earth and back. It lasts 6 years and on earth 10 years have passed.
The ship carries its own clock and also a computerized clock that always shows the time on earth at that moment.
It is about knowing the T - T' graph that the computer clock in the ship shows during the trip. The events to follow are (t,x=0), the ticks of the clock in earth frame, which must have coordinates in any other frame.
In the simplified problem, instantaneous accelerations, with SR calculations, the graph could look like this:
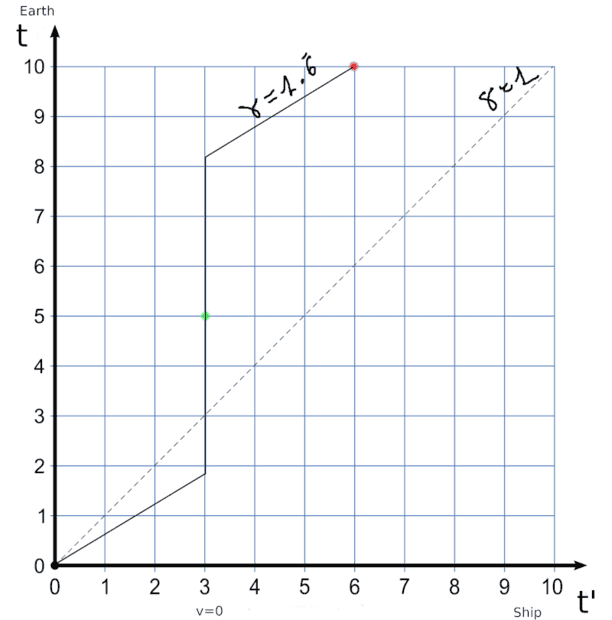 This graph represents several problems for me. One is the temporary discontinuity in the middle of the trip. The computerized clock that shows the time on earth would instantly change from marking about 2 years to marking about 8. And also this depends of pilot deciding to return. if he decides to continue flying away from Earth the computerized clock should not jump. All of this seems unphysical.
This graph represents several problems for me. One is the temporary discontinuity in the middle of the trip. The computerized clock that shows the time on earth would instantly change from marking about 2 years to marking about 8. And also this depends of pilot deciding to return. if he decides to continue flying away from Earth the computerized clock should not jump. All of this seems unphysical.
So I try to think of a more realistic graph, which takes into account the accelerations and following assumptions:
1. Every event, the ticks of the clock on earth, must have coordinates in other frames and its evolution must present continuity.
2. The accelerations (start, stop, return, stop) are symmetrical and must contribute equally to the graph.
And it seems to me that a realistic graph, with physical sense, should be like this.
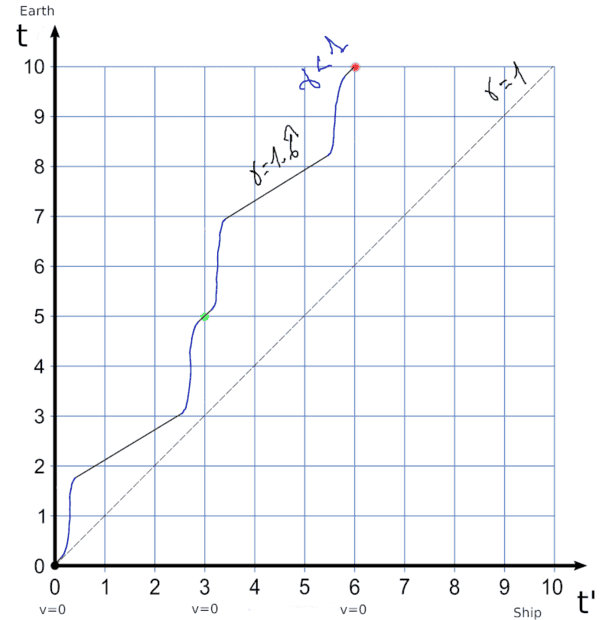
During the accelerations the slope is greater than 1. This indicates that the ship sees in the computerized clock that the time on earth is increasing very fast during the acceleration. This seems to be in accordance with GR equivalence principle. An acceleration, like a gravitational field, objectively slows down clocks.
When the ship is already going at a constant speed, the slope is less than 1. This indicates that it sees dilation in terrestrial time according to the Lorentz transformation.
When it stops halfway, the slope is 1 and the terrestrial clock follows the same rate.
However, according to SR, the acceleration does not influence, only the path and speed, and therefore there can be no slopes greater than 1 in this graph.
So I don't understand which of my assumptions is wrong. I would like to know what would be the right, realistic T-T' graph, the computerized clok in ship, in the twins paradox.
The ship carries its own clock and also a computerized clock that always shows the time on earth at that moment.
It is about knowing the T - T' graph that the computer clock in the ship shows during the trip. The events to follow are (t,x=0), the ticks of the clock in earth frame, which must have coordinates in any other frame.
In the simplified problem, instantaneous accelerations, with SR calculations, the graph could look like this:
So I try to think of a more realistic graph, which takes into account the accelerations and following assumptions:
1. Every event, the ticks of the clock on earth, must have coordinates in other frames and its evolution must present continuity.
2. The accelerations (start, stop, return, stop) are symmetrical and must contribute equally to the graph.
And it seems to me that a realistic graph, with physical sense, should be like this.
During the accelerations the slope is greater than 1. This indicates that the ship sees in the computerized clock that the time on earth is increasing very fast during the acceleration. This seems to be in accordance with GR equivalence principle. An acceleration, like a gravitational field, objectively slows down clocks.
When the ship is already going at a constant speed, the slope is less than 1. This indicates that it sees dilation in terrestrial time according to the Lorentz transformation.
When it stops halfway, the slope is 1 and the terrestrial clock follows the same rate.
However, according to SR, the acceleration does not influence, only the path and speed, and therefore there can be no slopes greater than 1 in this graph.
So I don't understand which of my assumptions is wrong. I would like to know what would be the right, realistic T-T' graph, the computerized clok in ship, in the twins paradox.