davidwinth
- 103
- 8
- Homework Statement
- This is not homework.
- Relevant Equations
- Sum of the forces equals zero, sum of the moments equals zero.
I am trying to figure out why the two approaches do not match in solving this statics problem. This involves the image below.
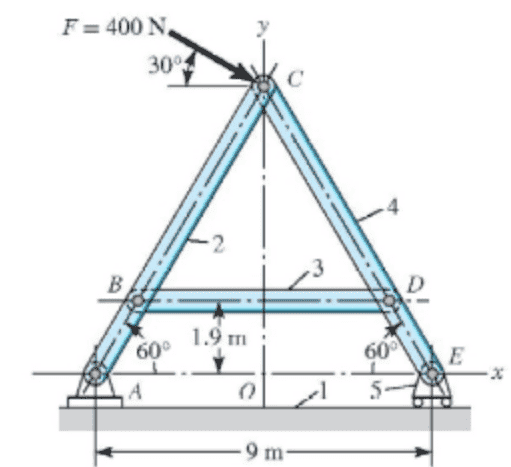
The first thing to do is to find the reactions at A and E. This is easy enough, with the results being that E only has a vertical component equal to 400 N and A has Ax = -346.4 N, Ay = -200 N. With this out of the way, we can find the force in CD and CB by using the method of joints.
Method of Joints on joint C.
##\sum F_x = 0 = 400cos(30)-F_{cd}cos(60)-F_{bc}cos(60)##
##\sum F_y = 0 = -400sin(30)+F_{cd}cos(60)-F_{bc}cos(60)##
Solving these leads to
##F_{cd} = 461.88 N##
##F_{bc} = 230.94 N##
So far so good. But now what if instead we look at individual members and solve the forces on them? Take member CDE for example. Here we only look at the reactions acting on the member. This includes the reactions at the pin at C, D, and E. A force balance on member CDE gives,
Method of Force Balance on Member CDE
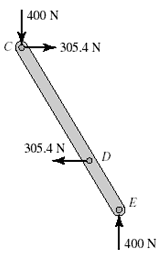
##R_D = 305.4N##
##R_{Cx} = 305.4 N##
##R_{Cy} = -400 N##
And we already found the reaction force at E. But here's where the trouble comes in. Say we take a cut between C and D to find the internal force in this member in order to see if it matches what we found by the Method of Joints. The internal force will have to balance with the reactions at C for equilibrium. Thus, we sum the projections of the components of the force at C along the member.
##F_{cd} = R_{cx}cos(60) + R_{cy}cos(30) = 499 N##
Thus the method of joints does not agree with the force balance approach. What have I missed?
Thanks.
The first thing to do is to find the reactions at A and E. This is easy enough, with the results being that E only has a vertical component equal to 400 N and A has Ax = -346.4 N, Ay = -200 N. With this out of the way, we can find the force in CD and CB by using the method of joints.
Method of Joints on joint C.
##\sum F_x = 0 = 400cos(30)-F_{cd}cos(60)-F_{bc}cos(60)##
##\sum F_y = 0 = -400sin(30)+F_{cd}cos(60)-F_{bc}cos(60)##
Solving these leads to
##F_{cd} = 461.88 N##
##F_{bc} = 230.94 N##
So far so good. But now what if instead we look at individual members and solve the forces on them? Take member CDE for example. Here we only look at the reactions acting on the member. This includes the reactions at the pin at C, D, and E. A force balance on member CDE gives,
Method of Force Balance on Member CDE
##R_D = 305.4N##
##R_{Cx} = 305.4 N##
##R_{Cy} = -400 N##
And we already found the reaction force at E. But here's where the trouble comes in. Say we take a cut between C and D to find the internal force in this member in order to see if it matches what we found by the Method of Joints. The internal force will have to balance with the reactions at C for equilibrium. Thus, we sum the projections of the components of the force at C along the member.
##F_{cd} = R_{cx}cos(60) + R_{cy}cos(30) = 499 N##
Thus the method of joints does not agree with the force balance approach. What have I missed?
Thanks.
Last edited: