abayerle
- 1
- 1
- TL;DR Summary
- Take two beams and bend one to a certain radius of curvature (maybe with a uniform load). Then take the second beam that is not bend and glue it onto the first. The glue is super stiff! Now how do I calculate the resulting curvature of the glued beams? How does the stress profile before and after gluing look like?
Thinking about Bernoulli Beam Theory and how to calculate the curvature of a beam, that you first bend and then glue to another beam. The latter is flat initially. How do I calculate the resulting curvature of the composite beam? How do I get the stress diagrams right - my first idea is in the image below.
Second scenario: Imagine you have glued the one beam to a very stiff, flat surface. Secondly you bend a second beam and then glue it on top of the other beam. In the third step you dissolve the glue layer of the first beam and now the composite beam is free to relax. It will curve, right? Is the curvature of the composite beam now different from that of the first scenario.
Ultimately, I want to think of a model where I stack many beams on top of each other and release the stack after all beams are fused.
Maybe someone closer to bending physics can help me out?
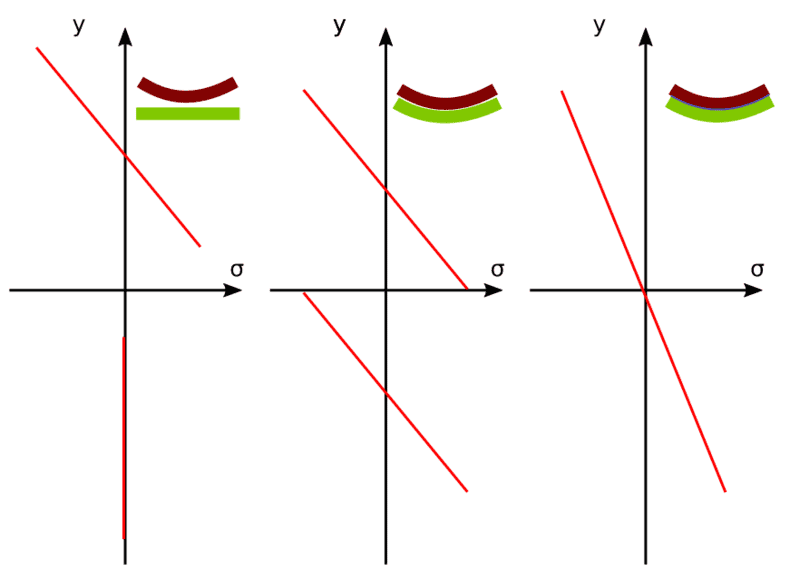
Second scenario: Imagine you have glued the one beam to a very stiff, flat surface. Secondly you bend a second beam and then glue it on top of the other beam. In the third step you dissolve the glue layer of the first beam and now the composite beam is free to relax. It will curve, right? Is the curvature of the composite beam now different from that of the first scenario.
Ultimately, I want to think of a model where I stack many beams on top of each other and release the stack after all beams are fused.
Maybe someone closer to bending physics can help me out?