- #1
member 508213
Homework Statement
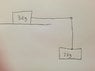
The problem is from a worksheet and is a picture so I will try to describe the picture. A 3kg block and a 7kg block are connected by a rope and the 7kg block is falling from a table and the 3kg block is on the table. We are supposed to find the acceleration of the 3kg block in the x direction assuming it is a frictionless area.
Homework Equations
f=ma
The Attempt at a Solution
My teacher told me it is 7m/s^2 and he explained why and I am trying to understand why his explanation is true.
First I will tell you what went through my head as I tried to solve this problem initially before I asked the teacher. I knew that the 7kg block was connected to the 3kg block by a rope and the 7kg block was falling and therefore pulling the rope which in turn would move the 3kg block. I knew that the mass was 7kg and that the acceleration due to gravity was causing it to fall at 9.8m/s^2 ( I will use 10m/s^2 for simplicity) so I calculated the force acting on the block to be 70N downward. From this I figured that if the block was falling with 70N of force then it must be pulling the rope with 70N which would be pulling the 3kg block at 70N. By this logic I calculated the acceleration with f=ma 70N=(3kg)(a) and calculated it to be (70/3) m/s^2. This is what I initially thought.
I will paraphrase what my teacher said: He explained that there is 70N of force, but it is acting on both objects and therefore we have to apply both the mass of the 3kg and the 7kg in the calculation, thus: 70N=10kg(a) and a would equal 7m/s^2. I am sure he is right I am not arguing that I am just having trouble accepting his explanation as true when I picture the situation as I stated above as 70N of force pulling a 3kg block. I need some help in order to picture what is happening differently so I can understand why this is true, because naturally I see the situation happening differently.
Any help is greatly appreciated.