- #1
GlennB
- 6
- 0
Hi all - I wonder if you could settle a dispute that's happening at a non-science forum? The maths itself seems complex, but the principle will be very familiar.
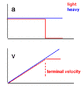
Two bodies are identical in every respect, except for mass (e.g. a solid steel ball and a hollow steel ball of the same dimensions)
They are dropped simultaneously, through the air, from a height such that neither reaches terminal velocity.
Does the heavier ball "pull away" from the lighter one in this scenario i.e. fall faster?
Or would it only "pull away" after the lighter one had reached terminal velocity?
Many thanks for your help
GlennB
Two bodies are identical in every respect, except for mass (e.g. a solid steel ball and a hollow steel ball of the same dimensions)
They are dropped simultaneously, through the air, from a height such that neither reaches terminal velocity.
Does the heavier ball "pull away" from the lighter one in this scenario i.e. fall faster?
Or would it only "pull away" after the lighter one had reached terminal velocity?
Many thanks for your help
GlennB