zenterix
- 774
- 84
- Homework Statement
- Two dielectrics with dielectric constants ##\kappa_1## and ##\kappa_2## each fill half the space between the plates of a parallel-plate capacitor as shown in the figure below.
Each plate has an area ##A## and the plates are separated by a distance ##d##.
Compute the capacitance of the system.
- Relevant Equations
- ##\oint_S\vec{E}\cdot\hat{n} dS=\frac{Q_{\text{enc}}}{\epsilon_0}##
We have a parallel plate capacitor with two different dielectrics
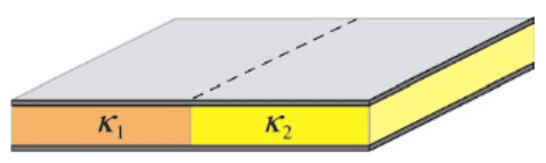
It seems to be the case that the potential difference on each half of the capacitor is the same.
Initially, the electric field was ##\vec{E_0}=\frac{2\sigma_+}{\epsilon_0}\hat{j}##.
If we were to insert a single dielectric material with dielectric constant ##\kappa_e## between the plates, this electric field would weaken to ##\frac{E_0}{\kappa_e}##.
The potential difference would also decrease to ##\frac{|\Delta V_0|}{\kappa_e}##.
But now we have two halves.
If the potential difference is the same in the two halves, then it must be that the electric fields are the same in the two halves. But then the charges on the halves must differ.
Does the reason the potential difference is the same on the two halves arise because of the path independence of ##\vec{E}##?
It seems to be the case that the potential difference on each half of the capacitor is the same.
Initially, the electric field was ##\vec{E_0}=\frac{2\sigma_+}{\epsilon_0}\hat{j}##.
If we were to insert a single dielectric material with dielectric constant ##\kappa_e## between the plates, this electric field would weaken to ##\frac{E_0}{\kappa_e}##.
The potential difference would also decrease to ##\frac{|\Delta V_0|}{\kappa_e}##.
But now we have two halves.
If the potential difference is the same in the two halves, then it must be that the electric fields are the same in the two halves. But then the charges on the halves must differ.
Does the reason the potential difference is the same on the two halves arise because of the path independence of ##\vec{E}##?