- #1
Thomasyar
- 1
- 0
(I) Find the limit (x,y)->(0,0) of F, then prove it by definition.
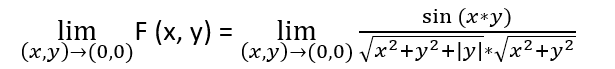
(II) Find the limit and prove it by definition of:
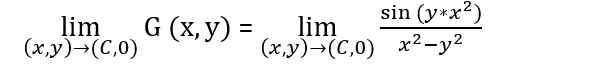
as (x,y) approach (C,0), C different from zero.
I have previously asked it on Quora, but it doesn't appear to have answers any time soon, and then I've encountered this forum.
--------------------
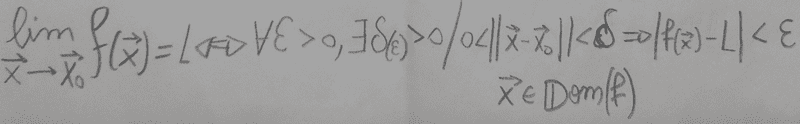
As every limit, the idea is to prove that it exist a positive Delta, which delimits the values of (x,y), for every Epsilon greater than zero. The common way to do it is to find a functional expression of Epsilon as a variable of the function Delta, where the domain of that function goes from zero to infinity, (0, +inf). Now, I have tried on both exercises multiple ways of findings relations between |(x,y)| and the corresponding function, all have failed.
In the second exercise the limit is obviously (0,0), due it doesn't have any discontinuity issue. But in the first one, I'm not totally sure if the limit exists. If it does, is (0,0).
The only thing that I explored deeply is delimiting the sine function as follows:
Abs(Sin(t)) <= Abs(t), and then t=x*y, since x <= |(x,y)| (same for y), so x*y <= |(x,y)|^2
(If 0 < C1 <= C3, and 0 < C2 <= C3, then C1*C2 <= C3*C2 <= C3^2; that’s what I used)
But that only lead me to have some sort of function of x and y in the denominator, and that is not useful.
(I managed to delimit |F(x,y)|<= 1/(sqrt(1+abs(y)))
Unless having some relation of the sort |F(x,y)|<= 1/J(x,y) is useful, I think gaining a relation of |(x,y)| in the denominator does not worth the try.
I would really appreciate it if someone gives me some help on proving those limits :)
(II) Find the limit and prove it by definition of:
as (x,y) approach (C,0), C different from zero.
I have previously asked it on Quora, but it doesn't appear to have answers any time soon, and then I've encountered this forum.
--------------------
As every limit, the idea is to prove that it exist a positive Delta, which delimits the values of (x,y), for every Epsilon greater than zero. The common way to do it is to find a functional expression of Epsilon as a variable of the function Delta, where the domain of that function goes from zero to infinity, (0, +inf). Now, I have tried on both exercises multiple ways of findings relations between |(x,y)| and the corresponding function, all have failed.
In the second exercise the limit is obviously (0,0), due it doesn't have any discontinuity issue. But in the first one, I'm not totally sure if the limit exists. If it does, is (0,0).
The only thing that I explored deeply is delimiting the sine function as follows:
Abs(Sin(t)) <= Abs(t), and then t=x*y, since x <= |(x,y)| (same for y), so x*y <= |(x,y)|^2
(If 0 < C1 <= C3, and 0 < C2 <= C3, then C1*C2 <= C3*C2 <= C3^2; that’s what I used)
But that only lead me to have some sort of function of x and y in the denominator, and that is not useful.
(I managed to delimit |F(x,y)|<= 1/(sqrt(1+abs(y)))
Unless having some relation of the sort |F(x,y)|<= 1/J(x,y) is useful, I think gaining a relation of |(x,y)| in the denominator does not worth the try.
I would really appreciate it if someone gives me some help on proving those limits :)