Ineedhelpwithphysics
- 43
- 7
- Homework Statement
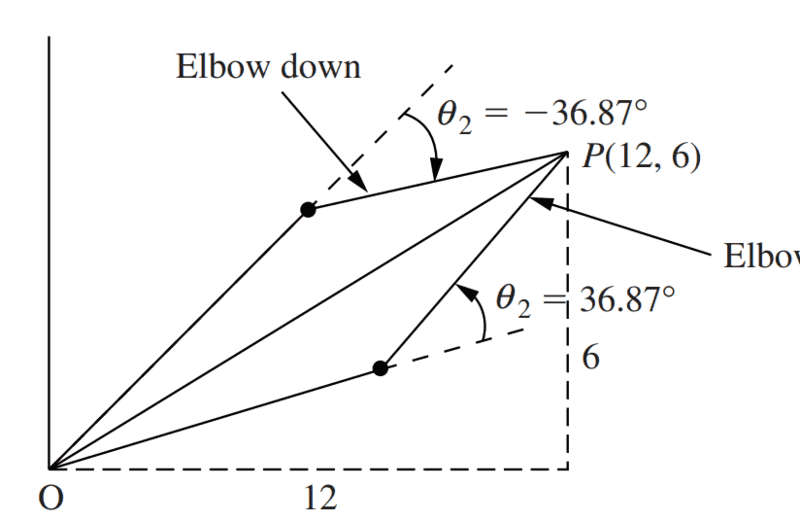
- The textbook is telling me this is elbow up but when I search on the internet it shows me something else.
- Relevant Equations
- law of cosines, law of sines, Pythagorean theorem
Textbook: vvvvv
Online: VVVV
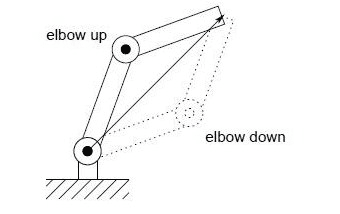
Online: VVVV