Two Masses, a Pulley, and an Inclined Plane help

[pcmarine]

Block 1, of mass m1, is connected over an ideal (massless and frictionless) pulley to block 2, of mass m2, as shown. Assume that the blocks accelerate as shown with an acceleration of magnitude a and that the coefficient of kinetic friction between block 2 and the plane is mu.

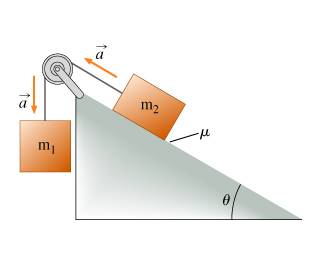
Find the ratio of the masses m1/m2.

 

[rammstein]

Let the tension in the thread be T. ok. now eq of motion of the 2 masses are...
(m1)g - T = (m1)a
T - (m2)gsin(theta) - (mu)(m2)gcos(theta) = (m2)a

Solving them by addng the two eqns u get,

m1/m2 = (g(sin(theta) + (mu)cos(theta)))/(g - a)

 

[pcmarine]

Thanks rammstein, but after inputting m1/m2, I get "aren't you missing a term?" Thanks a bunch for the help though!

 

[topsquark]

Thanks rammstein, but after inputting m1/m2, I get "aren't you missing a term?" Thanks a bunch for the help though!

That's right. The equations of motion are correct, he just dropped a term when he solved for m1/m2. Go ahead and solve the system and see what you get.

-Dan

 

[pcmarine]

I tried setting the two equations equal to each other through T, but was unable to discover the missing term...

 

[topsquark]

I tried setting the two equations equal to each other through T, but was unable to discover the missing term...

$$m_1g-T=m_1a$$ So $$T=m_1g-m_1a$$

$$(m_1g-m_1a)-m_2gsin \theta-\mu m_2gcos \theta=m_2a$$

$$m_1g-m_1a=m_2gsin \theta+\mu m_2gcos \theta+m_2a$$

$$m_1(g-a)=m_2(gsin \theta+\mu gcos \theta+a)$$

$$\frac{m1}{m2}=\frac{gsin \theta+\mu gcos \theta+a}{g-a}$$

rammstein left out the last "a" in the numerator.

-Dan