Two masses attached by a rod orbiting around the Earth

[(Ron)^2=-1]

Hello guys! I hope you can give me a hand with this one

Homework Statement

A satellite consisting of two masses attached by a rigid-massless rod of length L, are orbiting around the Earth at a distance R from the centre of the earth. During the entire movement the rod stays oriented in the radial direction. Consider the Earth to be stationary and the gravitational attraction between the masses to be negligible.

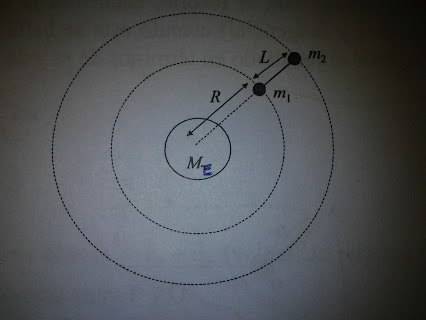A) Find the angular velocity of the satellite and the force the rod exerts on each mass.

Homework Equations

Force of gravity:

For mass 1→ Fg1= -G·Me·m1/R^2

For mass 2 → Fg2= -G·Me·m2/(R+L)^2​

The Attempt at a Solution

First thing I did was to consider the angular frequency of both masses to be the same, so:

For mass 1 → T1 = 2π/ω1

For mass 2→T2 = 2π/ω2​

Thus angular velocity ω must be the same for both masses, (is this correct?)

From the conservation of angular momentum (as there is no net torque), considering the centre of momentum to be the centre of the earth, I have the following:

L=L1+L2 ⇒ L=(m1·R^2 + m2·(R+L)^2)·ω​

And as L is constant then:

ω=L/(m1·R^2 + m2·(R+L)^2)
​

Finally from the equations of motion I got:

For mass 1→ ∑F = Fg1 + Tension1 = m1·a=m1·R·ω^2

For mass 2→ ∑F = Fg2 + Tension2= m2·a=m2·(R+L)·ω^2
​

So, from this two equations I seem to have everything I need, but I think I'm missing something here and I just can't see what it is

​

Thank you guys for your help!

​

 

[mfb]

Thus angular velocity ω must be the same for both masses, (is this correct?)

Sure.

I don't think introducing angular momentum helps, as you do not know its value.

You can express the accelerations (they will be different) in terms of the angular velocity and the given distances.

 

[(Ron)^2=-1]

Thanks for your help!

You can express the accelerations (they will be different) in terms of the angular velocity and the given distances.

That's really helpful. So from both equations I'll get:

For mass 1→a1 = R·ω^2
For mass 1 →a2 = (R+L)·ω^2
​

and then

Tension1 = (G·Me/R^2 + R·ω^2)·m

Tension2 = (G·Me/(R+L)^2+(R+L)·ω^2)·m

(m1=m2=m)
​

But are tension 1 and 2 the same (in absolute value) but opposite? If so then I think that's all, I can sum the two equations above and solve for ω and then replace to find the tension.

Praise be unto He

 

[mfb]

But are tension 1 and 2 the same (in absolute value) but opposite?

Sure.

If so then I think that's all, I can sum the two equations above and solve for ω and then replace to find the tension.

Right.

Helium is important!

 

[(Ron)^2=-1]

Great, thank you!

I agree, Helium is important!