Two masses on a rotating platform

[robtum]

Homework Statement

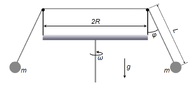
Two masses m are attached to opposite ends of an ideal piece of string
(massless, flexible) that rests on two frictionless, massless pulleys. The pulleys are fixed
to a rotating platform. The masses are stable when the platform stands still (does not
rotate), and the string hangs vertically from the pulleys. The platform is then carefully
rotated about the axis in the middle, such that the two ends of the string both form the
same angle φ with respect to vertical.
[Numerical values: m = 0.5 kg; R = 0.3 m; L = 0.6 m; g = 9.8 m/s2]

(a) What is the tension in the string when the masses hang vertically, i.e. before the platform starts rotating?
(b) Find the angular velocity ω so that the angle φ = 60◦.
(c) What is the tension in the string given the conditions in (b)?

Relevant Equations

U = mgh
v = ωr
a = ω^2 r
K = 1/2 m v^2

I'm having some trouble figuring this problem out. I've found the tension in (a) but I don't know where to start with (b). I've found that the distance between one of the masses and the rotational axis on the picture is R+0.52 m and that the masses rise to a height of h = 0.3 m.

The moment of inertia for the platform isn't given, so I don't know how to figure out the angular velocity. I tried using conservation of energy, that is 1/2 m v^2 = 2mgh, and the formula v = ωr. I've also tried using the tension in the strings, so that ω = sqrt((T sin(φ))/(m(R+0.52))) where T is the tension in the string but that value of ω doesn't match up with the value I get using conservation of energy. Any ideas on what I've done wrong?

 

[kuruman]

Maybe you don't need the moment of inertia of the platform. I suggest that you draw and analyze a free body diagram (FBD) of one of the masses when its string is at the given angle.

Why do you think energy is conserved? From what point A to what other point B is kinetic plus potential energy the same?

 

[robtum]

Maybe you don't need the moment of inertia of the platform. I suggest that you draw and analyze a free body diagram (FBD) of one of the masses when its string is at the given angle.

How did you use energy conservation, from what point A to what other point B?

Point A would've been when the masses are at rest like in part (a) and B is when the platform is rotating and the string is at the given angle. I realize now that the mechanical energy most likely isn't conserved at those two points though. There must be some work put into the system to make it rotate thus changing the mechanical energy, right? So would the better method be finding the centripetal force using a FBD and using the centripetal acceleration to find the angular velocity?

 

[kuruman]

So would the better method be finding the centripetal force using a FBD and using the centripetal acceleration to find the angular velocity?

Yes.