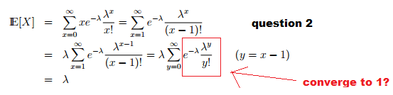- #1
nacho-man
- 171
- 0
Please refer to the attached images.
For question 2,
How does this converge to one? i tried using a ratio test but thought it converged to zero
For question 3,
I understand how they get a $\frac{1}{1+b-a}$ in the denominator, but not how they set up the rest.
for example if Y = min(0,X)
then Y>0 is impossible because the min(0,X) restricts the value of Y to 0. Thus making $P(Y>0) = 0$
Similarly, $P(Y<a) = 0$ since the bounds are restricted from $a<0<b$.
for $y=0$ this can occur when X takes any value over $[0,b]$. There are $b+1$ such values.
However, for $a<y<0$, aren't there $0-a+1$ such values? Why do they simply have a $1$ in the numerator.
For question 2,
How does this converge to one? i tried using a ratio test but thought it converged to zero
For question 3,
I understand how they get a $\frac{1}{1+b-a}$ in the denominator, but not how they set up the rest.
for example if Y = min(0,X)
then Y>0 is impossible because the min(0,X) restricts the value of Y to 0. Thus making $P(Y>0) = 0$
Similarly, $P(Y<a) = 0$ since the bounds are restricted from $a<0<b$.
for $y=0$ this can occur when X takes any value over $[0,b]$. There are $b+1$ such values.
However, for $a<y<0$, aren't there $0-a+1$ such values? Why do they simply have a $1$ in the numerator.