Two Particles Connected by Massless Rod: Dynamics Analysis

[Booze]

Homework Statement

The particle of mass M collapses with the body of two point-like particles of mass m.

Relevant Equations

Help needed

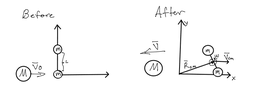
Two point-like particles of mass m. The particles are rigidly connected to each other with a mass-less rod of length L. The particles are initially at rest in such a way that one particle is at the origin and the other is at the point (0, L). A point-like particle of mass M collides with a particle located at the origin with a speed 𝑣⃗0.

a) After the collision, a particle of mass M bounces straight back to its direction of entry. Show that two m-the center of mass of the body formed by the particle must then move so that 𝑉𝑐𝑚 = 𝑀(𝑣0+𝑣)/2𝑚 .
b) Determine the orbital angular momentum 𝐿⃗⃗ 𝑡𝑟𝑎𝑛𝑠 and the rotation rate 𝐿⃗⃗ 𝑟𝑜𝑡 of the given
using quantities (relative to the origin) before and after the collision. What can you say about the total angular momentum value?
c) Show that after the collision, the body of two m-particles rotates counterclockwise with angular velocity 𝜔 = 𝑀(𝑣0+𝑣)/𝑚𝐿.

 

[BvU]

Hello @Booze ,

$\qquad$ !​

Please read the PF homework guidelines. We can only help if you post your attempt at solution.

What have you learned so far that can help you solve this one ?

Oh, and "Help needed" is NOT a relevant equation.

$\$

 

[Booze]

in question a) I don't get where does come from M(v0+v)!
i did the law of conservation of momentum before=after. i got that 2m is equel M, but i think it is wrong!
in b) i assumed before collision that Lrot is 0 and Ltrans= r(M) x p(M). and after collision i was thinking that Ltrans=r'(M) x p(M) + Rcm x p(body)=r'(M) x M*v0 +Rcm x Vcm*2m= Rcm*Vcm*2m - r'(M)*M*v=...=LM(v0+v)/m-r'(M)Mv
Vcm u know from a) and i calculate Rcm=mL/2m
i got c) right w=Vcm/Rcm= answer

 

[kuruman]

in question a) I don't get where does come from M(v0+v)!
i did the law of conservation of momentum before=after. i got that 2m is equel M, but i think it is wrong!
in b) i assumed before collision that Lrot is 0 and Ltrans= r(M) x p(M). and after collision i was thinking that Ltrans=r'(M) x p(M) + Rcm x p(body)=r'(M) x M*v0 +Rcm x Vcm*2m= Rcm*Vcm*2m - r'(M)*M*v=...=LM(v0+v)/m-r'(M)Mv
Vcm u know from a) and i calculate Rcm=mL/2m
i got c) right w=Vcm/Rcm= answer

Please show how you got your result in part (a), specifically how you applied linear momentum conservation. In part (b) you need to consider angular momentum conservation. What is the total angular momentum about the origin before the collision? Hint: $\mathbf{L}=\mathbf{r}\times\mathbf{p}$. Part (c) will sort itself out after you have obtained correct answers for parts (a) and (b).

 

[haruspex]

I don't get where does come from M(v0+v)!

Neither do I unless you are told that M bounces back with speed v (i.e. a velocity -v). Did you leave that out or is it missing from the original?

 

[kuruman]

Neither do I unless you are told that M bounces back with speed v (i.e. a velocity -v). Did you leave that out or is it missing from the original?

I had the same question about the meaning of v. Then I saw in the figure posted in #1 that M is shown bouncing back with speed v.