Two particles on a vertical ring

[EmmanuelE]

Homework Statement

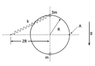
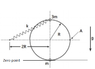
In this problem, I have two particles that slide on a ring with a radius of R. The ring is orientated in a vertical plane. One of the particle is heavier than the other and has a mass of 3m. The heavier particle is attached to a spring with an unstrectched length of 0 and a spring constant of k. The fixed end is attached at a distance of 2R from the center (see attached photo).

Homework Equations

The Attempt at a Solution

I need to work out the following:

1) The kinetic and potential energy of the heavy particle in the initial state, when it passes the left most position, horizontal with respect to the center of the circle, and when it hits the light particle.

2) The velocity of the heavy particle when it hits the light particle, and their joint velocity after their collision

3) What is the work done by gravity and the work done by the spring on the masses (mass=4m) from the release of the heavy particle until they both stop at point A in the figure?

Part 1)

At the highest point, the heavy particle has a kinetic energy of K = 0, since it is stated that the particle is at rest. The potential energy is different from 0, and it both has a gravitational potential energy (mgh) as well as an elastic/spring energy. The total potential energy for the heavy particle is given my U = U_k + U_h, where U_h is the potential energy due to gravity and U_k is the potential energy due to the spring.

I set my coordinate system, so the zero point is where m is on the figure, so I have the following:
U_h = mgh = 3∙m∙g∙2∙R = 6∙m∙g∙R

U_k = 1/2∙k ∙ x^2 = 1/2∙k ∙ 〖(√5R)〗^2 = 5/2∙k ∙ R= 5kR/2,
where x is the length of the spring and k is the elastic constant

The total potential energy for the heavy particle in its initial state is then:
U = U_k + U_h = (6∙m∙g∙R) + 5/2∙k ∙ R

When the particle is in the leftmost position, we have the following:
U_h = 3∙m∙g∙R
U_k = 5kR/2

To find the potential energy in this point, we use the conservation of energy:
K_start + U_start = K_left + U_left

Since the particle is at rest in the beginning, we have K_start = 0:
K_left = U_start – U_left
K_left = (6∙m∙g∙R + 5/2∙k ∙ R) - 3∙m∙g∙R
K_left = 3∙m∙g∙R + 2kR

That is what I have done so far.

For part 2)

When I find an expression for the kinetic energy when the masses collide, I can use that to solve for v in the equation and find the velocity.

For part 3)

The work done by a conservative force (we have no non-conservative forces in this problem) is equal to the negative change in potential energy. So to solve this problem, I need to find an expression for the potential energy. In part 1), we got the following expression: U_h = mgh = 6*m*g*R, which gives us the work done by gravity from the initial point until the masses collide and they stick together. Now, we are asked to find the work done by gravity until both masses are at point A, so can I use this expression to find the work done until point A and how?

As for the spring, I need to find an expression for the potential energy in point A and how?That was my reasoning for solving the problem. Now, am I on the right track, and if yes, how do I tackle the rest of the problem?

 

[mfb]

U_k = 1/2∙k ∙ x^2 = 1/2∙k ∙ 〖(√5R)〗^2 = 5/2∙k ∙ R= 5kR/2,
where x is the length of the spring and k is the elastic constant

Check the powers of R.

When the particle is in the leftmost position, we have the following:
U_h = 3∙m∙g∙R
U_k = 5kR/2

I guess U_k has a typo as you got it right later.

K_left = (6∙m∙g∙R + 5/2∙k ∙ R) - 3∙m∙g∙R

Same here.

When I find an expression for the kinetic energy when the masses collide, I can use that to solve for v in the equation and find the velocity.

Sure. Some of it can be taken from the last part of question 1 (not yet done).

Now, we are asked to find the work done by gravity until both masses are at point A, so can I use this expression to find the work done until point A and how?

You'll need part 2, and work from there, as the collisions seems to be inelastic.

 

[EmmanuelE]

Now I have:
U_k = (5 * k * R^2) / 2

and

K_left = (6*m*g*R + (5 * k * R^2) / 2) - 3*m*g*R = (5 * k * R^2) / 2 + 3*g*m*R

Now, that is the kinetic energy in the leftmost position. I need the kinetic and potential energy when it hits the light particle as well,

 

[TSny]

K_left = (6*m*g*R + (5 * k * R^2) / 2) - 3*m*g*R = (5 * k * R^2) / 2 + 3*g*m*R

Now, that is the kinetic energy in the leftmost position.

Does the spring have any potential energy at the leftmost position? Did you account for it?

 

[EmmanuelE]

Does the spring have any potential energy at the leftmost position? Did you account for it?

When we are in the leftmost point, we only know the potential energy:
U_h = 3mgR and U_k = 1/2 * k * R^2

We use conservation of energy, so the energy the particle had at the start is conserved:
K_start + U_start = K_left + U_left

K_start = 0, since the particle is at rest, so we have:
K_left = U_start - U_left = (6mgR + (5kR^2) / 2)) - (3mgR + (kR^2) / 2 = 2kR^2 + 3gmR

I the above equation, I inserted:
U_start = U_h (start) + U_k (start) = 6mgR + (5kR^2) / 2

Here U_h (start) is the potential energy due to gravity in the starting position and U_k (start) is the potential energy from the spring.

U_left = U_h (left) + U_k (left) = 3mgR + (kR^2) / 2

Here U_h (left) is the potential energy due to gravity in the leftmost position and U_k (left) is from the spring.

Now, I believe that I have accounted for the potential energy (spring) at the leftmost position.

 

[mfb]

U_k = 1/2 * k * R

Again, check the powers of R...
Please be a bit more careful with the expressions you a write down, that speeds up the solving process.

 

[EmmanuelE]

Again, check the powers of R...
Please be a bit more careful with the expressions you a write down, that speeds up the solving process.

That should be corrected now.

 

[mfb]

That looks better.

Now that you have the top and left position, what about the bottom before the collision?

 

[EmmanuelE]

That looks better.

Now that you have the top and left position, what about the bottom before the collision?

My zero point goes through m (the bottom of the ring), so the potential energy in the bottom of the ring must be 0.

 

[mfb]

There is not only the gravitational potential.

 

[EmmanuelE]

There is not only the gravitational potential.

So the potential energy due to gravity must be 0, while the spring potential energy is different from zero. We have:
U_h (bottom) = mgh = 0

U_k (bottom) = 1/2 * k * x^2 = (5kR^2) / 2

 

[EmmanuelE]

I tried to solve the rest of the question. Now that I have found the potential energy at the bottom, I am going to calculate the velocity of the heavy particle when it hits the light particle, and their joint velocity after the collision. First we look at the velocity of the heavy particle:

I want to find an expression that links the potential energy at the bottom to the kinetic energy:
PE = U_h (bottom) + U_k (bottom) = KE = 1/2 * m * v^2

Inserting in the above equation, we have:
(5kR^2) / 2 = 1/2 * m * v^2

I solve the equation for v, and I get:
v = sqrt( (5*k*R^2) / m )

Which is the velocity of the heavy particle when it hits the light particle.

Now I want to find their joint velocity and I want to use the following formula for an inelastic collision:
m₁*v₁=(m₁+m₂)*v₂

I solve the equation for v₂ and get:
v₂ = (m₁*v₁) / (m₁ + m₂)

Inserting the symbols from the illustration in the equation above, we get:
v₂ = (3 * R * sqrt( (5*k) /m)) / 4

Which is the joint velocity after the collision.

 

[mfb]

PE = U_h (bottom) + U_k (bottom) = KE

Why do you expect the two to be equal?

 

[EmmanuelE]

Why do you expect the two to be equal?

Since all of the potential energy (for the heavy particle) that it had in its initial position is converted to kinetic energy just before the collision.

 

[mfb]

You didn't even include the initial potential energy in that calculation.
Not all the potential energy of that position is converted to kinetic energy. There is some potential energy left at the bottom.

 

[EmmanuelE]

You didn't even include the initial potential energy in that calculation.
Not all the potential energy of that position is converted to kinetic energy. There is some potential energy left at the bottom.

Can we agree that I have the following potential energy and kinetic energy, where U_h is contribution to the total potential energy from gravity, and U_k is the contribution to the total potential energy from the spring. My zero point for the potential energy is in the bottom of the ring:

In the top where the heavy particle is at rest:
Potential energy:
U_h (start) = mgh = 3mg2R = 6mgR
U_k (start) = (1/2)*k*x^2 = (1/2)*k*sqrt(5)*R = (5*k*R^2) / 2

Total potential energy in the top of the ring therefore is: U_top (total) = U_h (start) + U_k (start) = 6mgR + 5*k*R^2) / 2

Kinetic energy:
K = 0 (the heavy particle is at rest)

In the leftmost position:
Potential energy:
U_h (left) = mgh = 3mgR
U_k (left) = (1/2)*k*x^2 = (1/2)*k*R^2

The total potential energy in the leftmost position of the ring therefore is: U_left (total) = U_h (left) + U_k (left) =3mgR + (1/2)*k*R^2

Kinetic energy:
K_left = U_start - U_left = (6mgR + (5kR^2) / 2)) - (3mgR + (kR^2) / 2 = 2kR^2 + 3gmR

In the bottom of the ring:
Potential energy:
U_h (bottom) = mgh = 0
U_k (bottom) = (1/2)*k*x^2 = (5kR^2) / 2

The total potential energy in the bottom position of the ring therefore is: U_bottom (total) = U_h (bottom) + U_k (bottom) = 0 + (5kR^2) / 2

Kinetic energy:
K_bottom = U_start - U_bottom = (6mgR + (5kR^2) / 2)) - ((5kR^2) / 2) = 6mgR

I used the conservation of energy to calculate the kinetic energy in the leftmost position and bottom of ring, since the total mechanical energy is total (we do not lose energy due to friction ect). Therefore, what we lose in potential energy must be equal to what we gain in kinetic energy, or the mechanical energy could not be total.Assuming that the above is correct, I want to calculate the velocity of the heavy object just before it hits the lighter particle in the bottom of the ring. Since I have just found an expression for the potential energy in the bottom of the ring (U_bottom), I want to use that to find my kinetic energy. My zero point for the potential energy goes through m, so all of the potential energy that the heavy particle initially had, must have been converted to kinetic energy just before the collision, since the mechanical energy is constant, since we not account for the friction in this problem. Therefore, I can write:

U_bottom (total) = K_bottom

Inserting into the equation we have:
(5kR^2) / 2 = (1/2)*m*v^2

Where v is the target variable. We solve the equation for v and get two solutions, where we use the positive:
v = (k*R*sqrt(5)) / sqrt(m)

Which is the velocity of the heavy particle just before the collision.

Now I want to find the joint velocity of the new object (mass 4m) after the collision. Since we have an inelastic collision, I use the following formula, where m₁ is the heavy particle and m₂ is the light particle:
m₁*v₁ + m₂*v₂ = (m₁ + m₂)*v_f

I solve the equation for v_f and get:
v_f = (m₁v₁+m₂v₂) / (m₁ + m₂)

Inserting the known data into the equation I get the following in the end:
v_f = (15 * sqrt(5) * R) / (4 * sqrt(m))

That was my reasoning behind my calculations.

 

[mfb]

I used the conservation of energy to calculate the kinetic energy in the leftmost position and bottom of ring, since the total mechanical energy is total (we do not lose energy due to friction ect). Therefore, what we lose in potential energy must be equal to what we gain in kinetic energy, or the mechanical energy could not be total.

Right so far.

Assuming that the above is correct, I want to calculate the velocity of the heavy object just before it hits the lighter particle in the bottom of the ring. Since I have just found an expression for the potential energy in the bottom of the ring (U_bottom), I want to use that to find my kinetic energy.

You found the kinetic energy already.

My zero point for the potential energy goes through m, so all of the potential energy that the heavy particle initially had, must have been converted to kinetic energy just before the collision

I don't know what you mean by "goes through m", but the heavy particle doesn't reach zero potential energy anywhere. You are going in the wrong direction here, you had the correct answer already.

U_bottom (total) = K_bottom

That is both wrong and in disagreement with the (wrong) argumentation before.

Inserting the known data into the equation I get the following in the end:
vf = (15 * sqrt(5) * R) / (4 * sqrt(m))

What happened to the factor k you had earlier? The earlier answer is wrong already, however.