- #1
RamosPinto
- 5
- 1
I'm currently trying to solve the following two-point boundary problem by means of the shooting method:
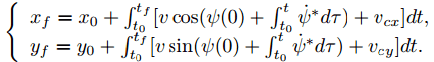
To clarify, I'm investigating the optimal route of aerial/marine vehicles from one point to another point, considering a flow field.
* The starting and ending locations are set as x0, y0 and xf, yf respectively.
* v is the constant speed of the vehicle relative to the field.
* A vector v=[vcx,vcy]T is used to describe the drift velocity of the field with respect to some coordinate system fixed to the ground.
* ψ is the vehicles navigation angle.
* The optimal change rate of the navigation angle has been found and is as follows:
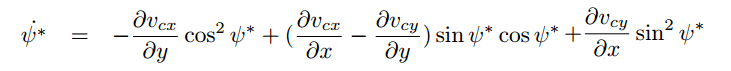
There are two unknowns in this two-point boundary value problem, which are the initial navigation angle ψ(0) and tf, which is the final time.
The problem that I would like some help with is thus the two-point boundary value problem that I want to solve by means of the shooting method. I haven't found useful and applicable sources that show me how to use the shooting method for this problem. I would very much appreciate a help in the right direction, either by some explanation or my directing me to useful sources.
Kind regards,
Ramos Pinto
To clarify, I'm investigating the optimal route of aerial/marine vehicles from one point to another point, considering a flow field.
* The starting and ending locations are set as x0, y0 and xf, yf respectively.
* v is the constant speed of the vehicle relative to the field.
* A vector v=[vcx,vcy]T is used to describe the drift velocity of the field with respect to some coordinate system fixed to the ground.
* ψ is the vehicles navigation angle.
* The optimal change rate of the navigation angle has been found and is as follows:
There are two unknowns in this two-point boundary value problem, which are the initial navigation angle ψ(0) and tf, which is the final time.
The problem that I would like some help with is thus the two-point boundary value problem that I want to solve by means of the shooting method. I haven't found useful and applicable sources that show me how to use the shooting method for this problem. I would very much appreciate a help in the right direction, either by some explanation or my directing me to useful sources.
Kind regards,
Ramos Pinto