Two questions about Black body radiation

[vijayantv]

TL;DR Summary

questions about Black body radiation

I have questions about Black body radiation. see the attached image

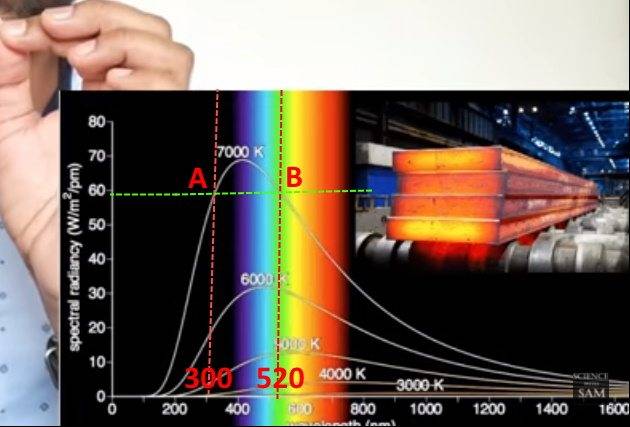
1). It explains that the Spectral radiance measurement of 7000K temperature is the same as both 300 and 520 nm wavelength light.
See here both A and B shows 60.
Is my understanding correct?

2). Is spectral radiance the number of photons? If not, what exactly it is?

Please clarify.

 

[haushofer]

1) Yes.

2) Looking at the units, I'd say the area under the curve denotes a power emitted per area. That's a number of photons per second per area.

 

[WernerQH]

2). Is spectral radiance the number of photons? If not, what exactly it is?

No, it is the radiated energy per square meter, per unit wavelength interval, and per unit of solid angle. At optical wavelengths it is rather unusual to express a wavelength interval in picometers. But you can write $60 \rm W m^{-2} pm^{-1} sr^{-1}$ also as $60 \rm kW m^{-2} nm^{-1} sr^{-1}$, or $6 \rm W cm^{-2} nm^{-1} sr^{-1}$.

The photon flux is different at the two wavelengths. Because 520 nm photons have lower energy than 300 nm photons, there must be more of them if the radiance is the same.

 

[vijayan_t]

No, it is the radiated energy per square meter, per unit wavelength interval, and per unit of solid angle. At optical wavelengths it is rather unusual to express a wavelength interval in picometers. But you can write $60 \rm W m^{-2} pm^{-1} sr^{-1}$ also as $60 \rm kW m^{-2} nm^{-1} sr^{-1}$, or $6 \rm W cm^{-2} nm^{-1} sr^{-1}$.

The photon flux is different at the two wavelengths. Because 520 nm photons have lower energy than 300 nm photons, there must be more of them if the radiance is the same.

Thanks for the reply.

When compare with 400 nm and 300 nm we get Spectral-radiance 70 and 60 respectively.

Here, the 300 nm photon has more energy than the 400 nm photon. how about the number of photons, in this scenario?

 

[WernerQH]

how about the number of photons, in this scenario?

You simply divide the spectral radiance by $h \nu (= hc / \lambda)$, the energy per photon, to get the flux of photons. You get a different curve because the factor is different for different wavelengths.

You have seen Planck's famous formula, haven't you? You can work out all numbers yourself using $$
I_\lambda = \frac {2 h c^2} {\lambda^5} \left(e^{hc/\lambda kT} - 1\right)^{-1}
$$ for the spectral radiance, and $$
\Phi_\lambda = \frac {2 c^2} {\lambda^4} \left(e^{hc/\lambda kT} - 1\right)^{-1}
$$ for the photon flux.

 

[vijayan_t]

You simply divide the spectral radiance by $h \nu (= hc / \lambda)$, the energy per photon, to get the flux of photons. You get a different curve because the factor is different for different wavelengths.

You have seen Planck's famous formula, haven't you? You can work out all numbers yourself using $$
I_\lambda = \frac {2 h c^2} {\lambda^5} \left(e^{hc/\lambda kT} - 1\right)^{-1}
$$ for the spectral radiance, and $$
\Phi_\lambda = \frac {2 c^2} {\lambda^4} \left(e^{hc/\lambda kT} - 1\right)^{-1}
$$ for the photon flux.

Got it. very clear ! .
Thanks .

 

[vanhees71]

You simply divide the spectral radiance by $h \nu (= hc / \lambda)$, the energy per photon, to get the flux of photons. You get a different curve because the factor is different for different wavelengths.

You have seen Planck's famous formula, haven't you? You can work out all numbers yourself using $$
I_\lambda = \frac {2 h c^2} {\lambda^5} \left(e^{hc/\lambda kT} - 1\right)^{-1}
$$ for the spectral radiance, and $$
\Phi_\lambda = \frac {2 c^2} {\lambda^4} \left(e^{hc/\lambda kT} - 1\right)^{-1}
$$ for the photon flux.

That's an important point, because that's indeed the only way to make physical sense of something like an average "photon number". One should be aware that what's physically measurable must be related to gauge independent local observables, and in the case of photons the measure related to intensity is energy density, which is both gauge invariant and a local observable, i.e., obeying the microcausality principle. That's not the case for a naive photon number density using the annihilation and creation operators of the mode decomposition of the free vector potential, because this is a gauge-dependent quantity, which does not fulfill the microcausality condition (in the radiation gauge).

 

[vijayan_t]

That's an important point, because that's indeed the only way to make physical sense of something like an average "photon number". One should be aware that what's physically measurable must be related to gauge independent local observables, and in the case of photons the measure related to intensity is energy density, which is both gauge invariant and a local observable, i.e., obeying the microcausality principle. That's not the case for a naive photon number density using the annihilation and creation operators of the mode decomposition of the free vector potential, because this is a gauge-dependent quantity, which does not fulfill the microcausality condition (in the radiation gauge).

Please explain in detail what is not correct in his explanation.
And Please provide your answer to my question.

Thanks

 

[PeterDonis]

see the attached image

Where is this image from? Please give a reference.

 

[PeterDonis]

Please explain in detail what is not correct in his explanation.

The "photon flux" in post #5 is not an actual number of photons. The state of the quantum electromagnetic field in this scenario is not even an eigenstate of photon number, so there is no definite "number of photons" at any frequency. At best the "photon flux" can be thought of as an expectation value of photon number for a given frequency.

Similar remarks apply to the "energy per photon" at a given frequency; this can't possibly be an actual energy per photon since there isn't even a definite number of photons present.

 

[PeterDonis]

Please provide your answer to my question.

What question of yours has not been answered?

 

[vanhees71]

Only gauge-invariant quantities from local observables have a physical interpretation. In the case of the electromagnetic field the photon-number operators do not fufill this criterion, because the field operators $\hat{\vec{A}}$ in the radiation gauge do not fulfill the microcausality condition, because of the constraint $\vec{\nabla} \cdot \hat{\vec{A}}=0$.

Observable are indeed intensities, i.e., the components of the energy-momentum tensor (particularly energy density and energy-current density/momentum density aka "Poynting vector"), because they derive from the physical field components $\vec{E}$ and $\vec{B}$ which fulfill microcausality conditions and are gauge invariant. So indeed "the flux", derived from the energy-current density of the em. field (Poynting vector) is an observable, but that must not be confused with a "photon-number current", which is not an observable. What you can define of course is the energy-current density divided by the energy and call this "photon-number current".

In the above quoted book by Zombeck it's of course done correctly, using the energy density ("radiance") as it must be.

 

[vanhees71]

Everybody understands "photon flux" as I said, namely as a count rate which is really measured. It's indeed defined via the Poynting vector and not some non-physical photon number, which indeed is a purely theoretical construct without any physically interpretible meaning.