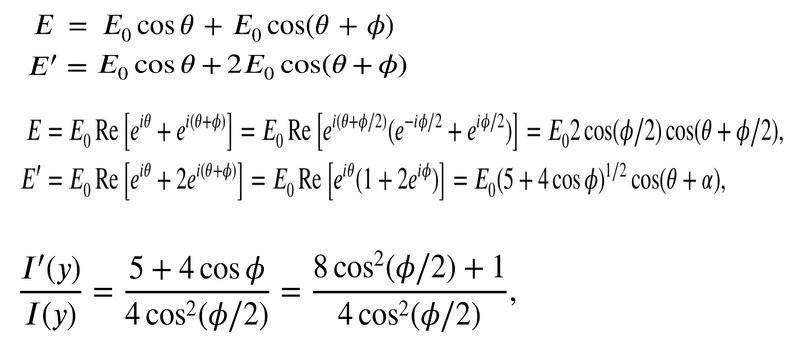maxim07
- 53
- 8
- Homework Statement
- A 2 slit interference pattern is viewed on a screen at distance R>>d from the plane of the slits where d is the slit spacing. If y is the transverse displacement across the screen, with y = 0 corresponding to the forward direction from the centre of the slits the intensity on the screen for small y is given by I = Icos^2(y*pi*d/wR), w is wavelength
If one of the slits is made twice as wide so that the amplitude of the point source has doubled show the intensity becomes
I’ = I/4(9cos^2(y*pi*d/wR) +1)
- Relevant Equations
- Cos(A) + cos(B) = 2cos(A+B/2)cos(A-B/2)
Here is the solution, I understand how they got E, but I don’t see how they could get E’ from cosine addition formulas? I don’t need to know how to do it with complex numbers.