kekpillangok
- 15
- 2
- Homework Statement
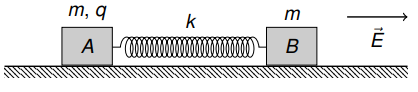
- The image shows two particles, A and B, attached to each other by a spring. Particle A has mass m and charge q; particle B has mass m and is electrically neutral. The spring has unstretched length l_0 and stiffness k. The system is in a region where there is an electric field E acting to the right. Neglecting friction and any electromagnetic radiation that may be emitted, find the position-time function for each particle given the following conditions:
1) When t = 0, particle A is at rest and passing through the origin of the coordinate system.
2) When t = 0, particle B is also at rest and is located at a distance l_0 from particle A.
- Relevant Equations
- F = ma
F_spring = -kx
X_cm = (x_1 * m_1 + x_2 * m_2) / (m_1 + m_2)
Here's what I've tried. First of all, I assume that q is positive. For particle A, then, I can write $$q E -k {\left( x _{A }-x _{B }\right) }=m \ddot{x }_{A }, $$ where ##x _{A } ## and ##x _{B } ## are the coordinates of the particles relative to their equilibrium positions from the point of view of the centre of mass. For particle B, I can write $$k {\left( x _{A }-x _{B }\right) }=m \ddot{x }_{B }. $$ Subtracting the second equation from the first gives $$q E -2 k {\left( x _{A }-x _{B }\right) }=m {\left( \ddot{x }_{A }-\ddot{x }_{B }\right) }. $$ Changing variables so that the equation has the form of a simple harmonic oscillator, I find that the angular frequency of oscillation relative to the centre of mass is $$\omega =\sqrt{\frac{2 k }{m }}. $$ This is the frequency with which each particle oscillates. Now I need to find the position-time functions for the particles, and this is where I get stuck. I know that ##x _{A }{\left( 0 \right) }=0 ## and ##x _{B }{\left( 0 \right) }=l _{0 } ##. I can also see that, at ##t =0 ##, the only force acting on particle A is the electric force, so ##\ddot{x }_{A }{\left( 0 \right) }=\frac{q E }{m } ##. Also, since there are no forces acting on particle B at that moment, I conclude that ##\ddot{x }_{B }{\left( 0 \right) }=0 ##, but this can't be particle B's equilibrium position relative to the centre of mass because its speed is zero at ##t =0## according to condition 2.
Adding the first two equations I wrote here gives $$q E =m {\left( \ddot{x }_{A }+\ddot{x }_{B }\right) }, $$ so ##a _{CM }, ## the acceleration of the centre of mass, must be equal to ##\frac{q E }{2 m } ##. The position-time function for the centre of mass, then, is $$x _{CM }{\left( t \right) }=\frac{l _{0 }}{2 }+\frac{q E }{4 m }{t }^{2 }, $$ which should be progress, but finding the position-time functions for the particles is giving me a headache. I can see that the whole system is accelerating to the right, and that it's the electric force that sets it all into motion and causes it to oscillate. There is no human being pulling the particles apart and releasing them to make them oscillate—it all starts from the electric force. I also imagine that the maximum speed of particle A relative to the centre of mass will be attained when the electric and elastic forces balance each other out; i.e., when $$x =\frac{q E }{k }. $$ ##x ## here refers to the total deformation of the spring. When the spring is deformed by that amount, then, particle A reaches its maximum speed. This need not, however, be the deformation at which B attains its maximum speed. Indeed, when A reaches its maximum speed, B is still being accelerated to the right because the elastic force is still pushing it to the right. So, when A is at its equilibrium position, ##\ddot{x }_{B }=\frac{q E }{m } ##, and I conclude that there is a phase difference in the oscillations of the two particles. When A is at maximum speed, B is still being accelerated; when A stops (relative to the centre of mass), B is at maximum speed.
I know, then, that, relative to the centre of mass, A will oscillate about the point ## x _{eq }=-\frac{l _{0 }}{2 }+\frac{q E }{2 k }.## This must be the case because the deformation of the spring is ##\frac{q E }{k } ## when the forces on A cancel each other out. Therefore A must have moved in towards the centre of mass by an amount ##\frac{q E }{2 k } ##. I should expect the position-time function for A relative to the centre of mass, then, to have the form $$ x {\left( t \right) }=-\frac{l _{0 }}{2 }+\frac{q E }{2 k }+A \cos \left( \omega t +\phi \right) \, .$$ Figuring out A (the amplitude of oscillation) is proving very difficult, however. If anyone can guide me through this one, I'll be very thankful.
Adding the first two equations I wrote here gives $$q E =m {\left( \ddot{x }_{A }+\ddot{x }_{B }\right) }, $$ so ##a _{CM }, ## the acceleration of the centre of mass, must be equal to ##\frac{q E }{2 m } ##. The position-time function for the centre of mass, then, is $$x _{CM }{\left( t \right) }=\frac{l _{0 }}{2 }+\frac{q E }{4 m }{t }^{2 }, $$ which should be progress, but finding the position-time functions for the particles is giving me a headache. I can see that the whole system is accelerating to the right, and that it's the electric force that sets it all into motion and causes it to oscillate. There is no human being pulling the particles apart and releasing them to make them oscillate—it all starts from the electric force. I also imagine that the maximum speed of particle A relative to the centre of mass will be attained when the electric and elastic forces balance each other out; i.e., when $$x =\frac{q E }{k }. $$ ##x ## here refers to the total deformation of the spring. When the spring is deformed by that amount, then, particle A reaches its maximum speed. This need not, however, be the deformation at which B attains its maximum speed. Indeed, when A reaches its maximum speed, B is still being accelerated to the right because the elastic force is still pushing it to the right. So, when A is at its equilibrium position, ##\ddot{x }_{B }=\frac{q E }{m } ##, and I conclude that there is a phase difference in the oscillations of the two particles. When A is at maximum speed, B is still being accelerated; when A stops (relative to the centre of mass), B is at maximum speed.
I know, then, that, relative to the centre of mass, A will oscillate about the point ## x _{eq }=-\frac{l _{0 }}{2 }+\frac{q E }{2 k }.## This must be the case because the deformation of the spring is ##\frac{q E }{k } ## when the forces on A cancel each other out. Therefore A must have moved in towards the centre of mass by an amount ##\frac{q E }{2 k } ##. I should expect the position-time function for A relative to the centre of mass, then, to have the form $$ x {\left( t \right) }=-\frac{l _{0 }}{2 }+\frac{q E }{2 k }+A \cos \left( \omega t +\phi \right) \, .$$ Figuring out A (the amplitude of oscillation) is proving very difficult, however. If anyone can guide me through this one, I'll be very thankful.