- #1
coldpay
- 5
- 0
Homework Statement
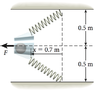
A horizontal slingshot consists of two light, identical springs (with spring constants of 24.1 N/m) and a light cup that holds a 1.21-kg stone. Each spring has an equilibrium length of 50 cm. When the springs are in equilibrium, they line up vertically. Suppose that the cup containing the mass is pulled to x = 0.7 m to the left of the vertical and then released. Determine
a) the system’s total mechanical energy.
b) the speed of the stone at x = 0.