joejoe121
- 17
- 2
- Homework Statement
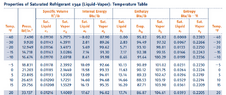
- Two tanks are connected by a valve and line. The volumes are both 1 cubic meter with R-134a at 20 C, quality 15% in tank A and tank b is evacuated. The valve is opened and saturated vapor flows from A into B until the pressures become equal. The process occurs slowly enough that all temperatures stay at 20 C during the process.
a) Initial specific internal energy in A is......kj/kg
b) Initial mass in A is.......kg
c) Final specific internal energy of R-134 is..........kj/kg
d) Total work during process is.......kj
e) Total heat transfer during the process is.......kg
- Relevant Equations
- u = u_f + x(u_g-u_f)
v= = v_f +x(v_g-v_f)
mass = V/specific volume
I've attached all my work and data table I used to answer the questions but there isn't an answer key so I would like a second opinion.


Attachments
Last edited: