- #1
Adrian555
- 7
- 0
Hi everybody,
This is my first post, so I apologise for all the possible mistakes that I can make now and in the future. I promise that I'll learn from them!
My question is the following: It's well-known the relationship between two pair of cartesian axes when a circular rotation is made:

Nevertheless, when dealing with a Minkowski rotation like this one:
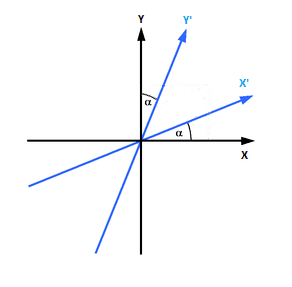
I was wondering if a relationship between the new (blue) and old (black) pair of axis as function of the circular angle alpha can be obtained (that is to say, without using an hyperbolic angle).
Thanks in advance for your help.
This is my first post, so I apologise for all the possible mistakes that I can make now and in the future. I promise that I'll learn from them!
My question is the following: It's well-known the relationship between two pair of cartesian axes when a circular rotation is made:
Nevertheless, when dealing with a Minkowski rotation like this one:
I was wondering if a relationship between the new (blue) and old (black) pair of axis as function of the circular angle alpha can be obtained (that is to say, without using an hyperbolic angle).
Thanks in advance for your help.