- #1
alex3
- 44
- 0
I'm numerically evaluating the differential cross sections [itex]\frac{\operatorname{d}\sigma}{\operatorname{d} \Omega}[/itex] for [itex]e^{-}e^{+}\rightarrow\mu^{-}\mu^{+}[/itex] scattering by integrating over [itex]\operatorname{d}\Omega = \operatorname{d}(\cos{\vartheta})\operatorname{d} \phi[/itex].
Assuming no transverse polarisation so that the integration over [itex]\phi[/itex] is simply [itex]2\pi[/itex], and also assuming no electron mass, there are three effective cross sections: one due solely to [itex]\gamma-\gamma[/itex], one due to [itex]Z^{0}-Z^{0}[/itex], and one due to the interference term of the matrix elements ([itex](\mathcal{M}_{\gamma} + \mathcal{M}_{Z^{0}})^{2}[/itex]), [itex]\gamma-Z^{0}[/itex]. The photon term is the so-called QED term, while the Z boson terms are the Standard Model terms.
I'm not experienced in plotting or analysing these kinds of events, so my problem is that I'm unsure of what to expect. I know that I should see a resonance, as I am, but I'm worried that the interference term should be contributing more than what I'm seeing.
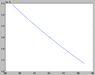
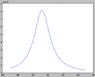
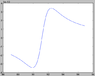
I've attached three plots, each centred around the [itex]Z^{0}[/itex] mass (which I've taken as about 91.2GeV). The first is the [itex]\gamma-\gamma[/itex] contribution, second the [itex]Z^{0}-Z^{0}[/itex], third the interference term [itex]\gamma-Z^{0}[/itex]. The fourth plot, the combined total cross section [itex]\sigma[/itex], can be found http://cl.ly/421W1Y212L0k3h0B0S27 . (These are raw plots! Energy in GeV on [itex]x[/itex], cross section [itex]\sigma[/itex] on [itex]y[/itex].)
As you can see, each contribution has a different form (which is OK), but the interference term is much smaller (~10e-3) than the dominating [itex]Z^{0}-Z^{0}[/itex] term. Is this expected behaviour for these types of events?
(I should mention that the given differential cross sections are trivially solvable. I think I have coded it up correctly, but given my inexperience it would be nice to hear from someone with more competence in the field.)
Assuming no transverse polarisation so that the integration over [itex]\phi[/itex] is simply [itex]2\pi[/itex], and also assuming no electron mass, there are three effective cross sections: one due solely to [itex]\gamma-\gamma[/itex], one due to [itex]Z^{0}-Z^{0}[/itex], and one due to the interference term of the matrix elements ([itex](\mathcal{M}_{\gamma} + \mathcal{M}_{Z^{0}})^{2}[/itex]), [itex]\gamma-Z^{0}[/itex]. The photon term is the so-called QED term, while the Z boson terms are the Standard Model terms.
I'm not experienced in plotting or analysing these kinds of events, so my problem is that I'm unsure of what to expect. I know that I should see a resonance, as I am, but I'm worried that the interference term should be contributing more than what I'm seeing.
I've attached three plots, each centred around the [itex]Z^{0}[/itex] mass (which I've taken as about 91.2GeV). The first is the [itex]\gamma-\gamma[/itex] contribution, second the [itex]Z^{0}-Z^{0}[/itex], third the interference term [itex]\gamma-Z^{0}[/itex]. The fourth plot, the combined total cross section [itex]\sigma[/itex], can be found http://cl.ly/421W1Y212L0k3h0B0S27 . (These are raw plots! Energy in GeV on [itex]x[/itex], cross section [itex]\sigma[/itex] on [itex]y[/itex].)
As you can see, each contribution has a different form (which is OK), but the interference term is much smaller (~10e-3) than the dominating [itex]Z^{0}-Z^{0}[/itex] term. Is this expected behaviour for these types of events?
(I should mention that the given differential cross sections are trivially solvable. I think I have coded it up correctly, but given my inexperience it would be nice to hear from someone with more competence in the field.)
Attachments
Last edited by a moderator: