Unable to show the radius of convergence of a numeric series

[aheight]

Hi,

I've computed 512 terms of a power series numerically. Below are the first 20 terms.

$$
\begin{align*}
w(z)&=0.182456 -0.00505418 z+0.323581 z^2-0.708205 z^3-0.861668 z^4+0.83326 z^5+0.994182 z^6 \\ &-1.18398 z^7-0.849919 z^8+2.58123 z^9-0.487307 z^{10}-7.57713 z^{11}+3.91376 z^{12}\\
&+19.6052 z^{13}-12.717 z^{14}-40.7957 z^{15}+40.3343 z^{16}+66.9766 z^{17}-133.148 z^{18}\\
&-78.9037 z^{19}+\cdots
\end{align*}
$$

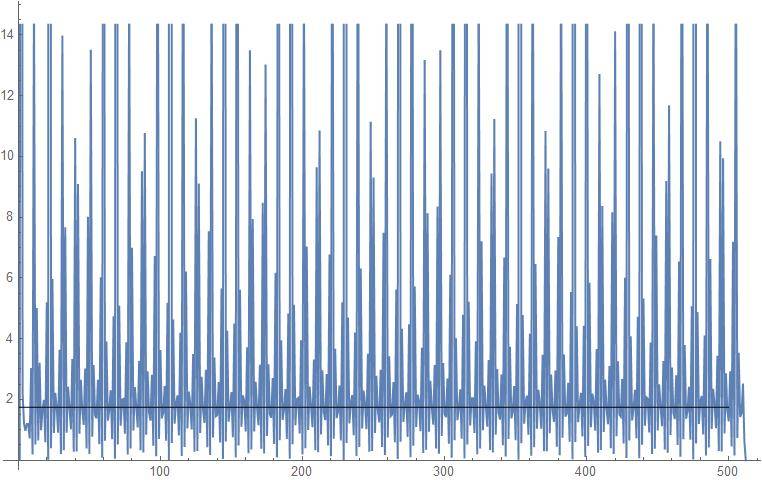
And wish to show the radius of convergence is approx $0.574342$. The Ratio test fails as successive ratios are finite but do not tend to a limit as shown in the plot below and I cannot use the Alternating Series test either or integral test or other convergence test I am aware of.

I was wondering if someone could suggest another method I could use to suggest experimentally that this series is appearing to converge (conditionally) in the indicated domain?

 

[scottdave]

What is the function generating the coefficients? It's difficult to tell what will happen just from these numbers. I cannot even see a pattern to say whether the next term will be positive or negative.

 

[jedishrfu]

What if you evaluate the odd terms only or the even terms only? Or evaluate with specific values of z like -2, -1, 1, 2 ... to see what you get?

 

[aheight]

The series is a Puiseux expansion at the origin of one of the four single-cycle branches of the function $w(z)$ given implicitly by:

$$
f(z,w)=(1+3 z^2-4 z^3-3 z^4)+(-5-6 z^2)w+(-3-8 z^4)w^2+(2-6 z-9 z^3)w^3+(6 z-9 z^3+7 z^4)w^4=0
$$

The other three series show nice numerical convergence to the expected value via the Ratio Test but this one does not: the ratios oscillate as shown in the pic above so I assume it's converging conditionally.

What if you evaluate the odd terms only or the even terms only? Or evaluate with specific values of z like -2, -1, 1, 2 ... to see what you get?

I evaluated 512 terms of the series at 300 digits of precision in the domain $|z|<0.5$ and compared it with the branch values and it compares nicely. Below is a comparison of the Re[series] results in red superimposed on the actual branch sheet in the domain $|z|<0.55$. Looks nice so that give me more confidence the convergence domain I stated is correct (other black figure in plot is another branch sheet with a smaller radius of convergence).

 

[jedishrfu]

Perhaps another mathematician like @fresh_42 can help here.

 

[Mark44]

What is the function generating the coefficients? It's difficult to tell what will happen just from these numbers.

This is my thought, as well. You can't tell much about a series just by a list of the numeric coefficients. Knowing how these numbers were generated is about the only way I can think of to figure out whether the series converges, or if it does, what the radius of convergence is.

Also, I have no idea what the graph in post #1 is supposed to convey.

 

[jedishrfu]

I think the plot is a bar chart of each term’s value in the polynomial expansion.

 

[aheight]

This is my thought, as well. You can't tell much about a series just by a list of the numeric coefficients. Knowing how these numbers were generated is about the only way I can think of to figure out whether the series converges, or if it does, what the radius of convergence is.

Also, I have no idea what the graph in post #1 is supposed to convey.

The terms are generated by an iterative procedure called Newton Polygon but the procedure does not provide a means of computing the region of convergence.

I think the plot is a bar chart of each term’s value in the polynomial expansion.

I am sorry for not being clear above about the plot: the plot lists the successive ratios $\frac{a_{n+1}}{a_n}$ of the power series $\sum_{n=0}^{N} a_n z^n$ for the Ratio Test. The plot below are the results of plotting these ratios for another branch of the function. Note how the ratios are tending approx to the point 8.499. Now when we substitute this into the Ratio Test we have $8.499 |z|<1$ for convergence so that the region of convergence is $|z|<0.117728$ which is already very close to the actual value of approx $0.1174$.

 

[aheight]

The Wikipedia article, "Radius of convergence" gives an unusual test for convergence:

Define the sequence: $$ b_n^2=\frac{c_{n+1}\; c_{n-1}-c_n^2}{c_n\; c_{n-2}-c_{n-1}^2}$$

and then plot the points $\{1/n,b_n\}$ and extrapolate linearly to the point $1/n=0$. The y-intercept of $1/n=0$ gives an estimate of the reciprocal of the radius of convergence. So i computed 1024 terms of the above series and obtained the plot below with a y-intercept of 1.74061 giving the estimated radius of convergence of 0.574513 which agrees with the predicted value above to 3 digits.

However, the citation for this test:

Mercer, G.N.; Roberts, A.J. (1990), "A centre manifold description of contaminant dispersion in channels with varying flow properties", SIAM J. Appl. Math., 50 (6): 1547–1565, doi:10.1137/0150091

is not publicly-available. I was wondering if anyone reading this would know where I could find out more information about this convergence test.