Uncertainty Error and Significant Figures in this Force Tables Lab

[Albertgauss]

TL;DR Summary: I have a Force Table Lab and am not sure if the "percent error" is the correct way to express errors. I also need some help on sig figs for my results.

Hello,

I am working with the usual undergrad force tables apparatus. I would like to know how to express the results of measurements and calculations properly for such an apparatus and make the measurements to the correct number of significant figures.

Here is a picture of the situation to show the beginning of the problem:

The ring is unbalanced by two masses, a 130 gram mass at 300 degrees and a 200 gram mass at 60 degrees. I calculate that I would need (using the usual force vector math) to hang a 175.78 gram mass at 200.17 degrees to balance the ring (such that it floats and does not touch the center peg). These are my theory values.

Here is a schematic of the situation.

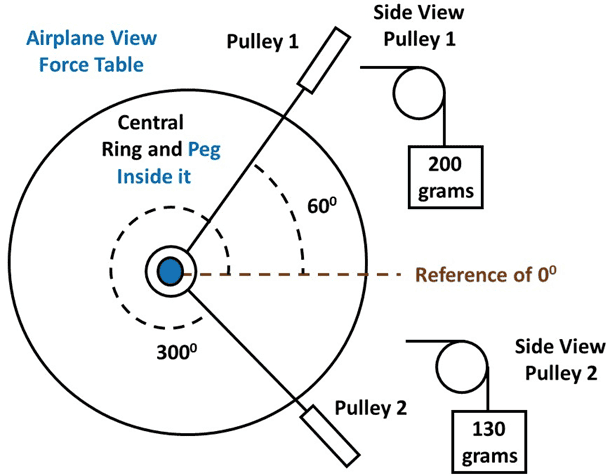
When I did the actual experiment, I measured that the mass to balance my system should be 180 grams at 194 degrees, and you can see that below.

In the left figure you can see that I can measure the angle no better reliably than to one degree; a finer increment than one degree on the force table and I can’t really measure that. In the right-hand side, those masses lumped together total 180 grams. I could put on little disks of one gram or so, but no masses smaller than that.

How do I properly express my measurements in terms of my limiting ability to measure the angle at no better than one degree or my mass to no better than one gram? I do have a percent error formula I can work with and it goes as follows:

100*Absolute Value of (theory value subtract experimentally measured value)/(theory value)

The percent error on the mass is 2.4% and the percent error on the angle direction is 2.6%. Would this suffice for error analysis or is there a better way to do it? How do I report these findings with correct significant figures?

 

[PeroK]

How do I properly express my measurements in terms of my limiting ability to measure the angle at no better than one degree or my mass to no better than one gram? I do have a percent error formula I can work with and it goes as follows:

100*Absolute Value of (theory value subtract experimentally measured value)/(theory value)

The percent error on the mass is 2.4% and the percent error on the angle direction is 2.6%. Would this suffice for error analysis or is there a better way to do it? How do I report these findings with correct significant figures?

The percentage error in the force seems okay, but it can't apply to angles. Suppose you rotate the table so that the expected angle is zero - instead of 200 degrees? Then the percentage error is either very large or infinite. Note that the error in the angle is unrelated to the magnitude of the expected angle. It makes little sense to express it as a percentage in this case. In fact, when I checked your calculations, I calculated the angle relative to the 180 degree line. My calculation was 20 degrees.

This is not my area of expertise, but you would need to try other configurations to see how the error in the angle changes. The weak point of the experiment, I suggest, is the angle at which the strings are attached to the small ring in the centre. A small displacement of the attachement point round the circumference of the ring won't make much difference to the force on the ring, but may make a relatively large difference to the effective angle at which the ring is being pulled. That, as far as I can see, equates effectively to an absolute uncertainty in angle. I.e. the two known forces might have a small percentage errror in magnitude of force, but a large absolute error in terms of angle. It might be plus/minus 5 degrees (regardless of whether the angle is 0 degrees or 359 degrees).

 

[Steve4Physics]

Various thoughts in addition to what @PeroK has already said.

Angles look like they could be measured ±0.5º (or even ±0.2º with care).

Your reading looks to be 196.0º, not 194º. Check it!

Measured angles in degrees should be recorded to 1 d.p.

Measured masses in grams should be recorded to the nearest gram.

Ideally you would have repeated the measurements a few times to get an average.

Ideally you would have measured the masses using an electronic balance to get more precise values.

The percent error on the mass is 2.4% and the percent error on the angle direction is 2.6%. Would this suffice for error analysis or is there a better way to do it? How do I report these findings with correct significant figures?

That’s just a comparison of predicted and measured values. It may be adequate - it depends on your course requirements for lab' write-ups at your stage in the course. [EDIT - but expressing the angle error as a percentage is dodgy - see later post #5.]

A more thorough approach requires an 'error propagation' analysis. This would give the expected ranges of the calculated mass and angle resulting from the uncertainties in the measurements. Check your course handbook or with your supervisor whether or not you need to do this. There are different techniques (at different levels of sophistication). You can do a search and some reading.

Without doing the error propagation analysis, I'd be tempted to give::
- the measured and predicted masses to the nearest 1gram and the % difference;
- the measured and predicted angles to the nearest 0.1º and the absolute difference between them.

 

[Albertgauss]

looks good. I don't want to get too complicated but I think the limits put forth here down to the nearest gram and tenth of an angle are the way to go. The percent error and just the human resolution here visually would be the easiest way to teach about errors and uncertainty, mostly just to get the students thinking about error and uncertainty but I don't know if more advanced error propagation techniques are really necessary for this kind of a lab. I did want to double check, though, and that seems to be confirmed here. I like the conclusion at the end of Steve4Physics.

Also, PeroK, good observations about how much the angle could vary. Yes, it looks right that the angle at which the string passes over the pulley is not as exacting as the experiment leads one to believe; there is much more uncertainty if one examines the angle where it originates on the ring.

Good points all, and I will incorporate these ideas accordingly.

 

[PeroK]

The percent error and just the human resolution here visually would be the easiest way to teach about errors and uncertainty, mostly just to get the students thinking about error and uncertainty ...

In this setup, a percentage error in angle is fundamentally wrong. The error has the same value (let's say $\pm$ 1 degree), regardless of which angle the string is at. Otherwise, you have a small error in a measurement of $-1$ degree, but a large error in a measurement of $359$ degrees - but these are the same angle. That point cannot be overlooked, IMO.