- #1
guyvsdcsniper
- 264
- 37
- Homework Statement
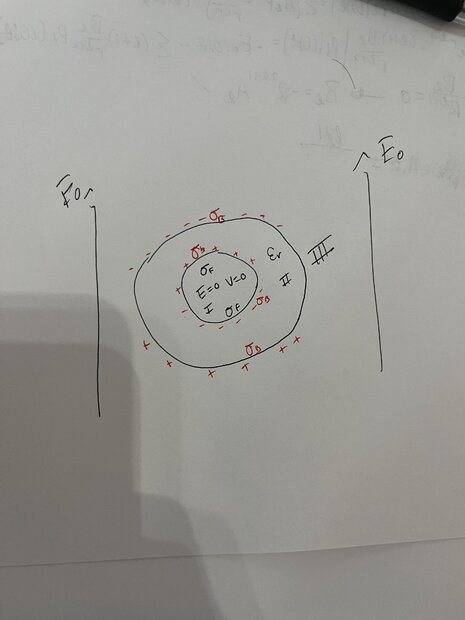
- An uncharged conducting sphere of radius a is coated with a thick
insulating shell (dielectric constant r ) out to radius b. This object is now placed in
an otherwise uniform electric field Eo. Find the dipole moment of the conductor.
- Relevant Equations
- p = ∫rσ(r)dA.
I worked this problem out in griffiths and my work checks out for for the potentials, b.c. and the coefficients. I will post the solutions just because my work is a little harder to read.
What I am having trouble finding is the dipole moment of the conductor.
I know the formula for dipole moment can be written as p = ∫rσ(r)dA.
Im stuck on how to find σ or if this formula is the right approach.
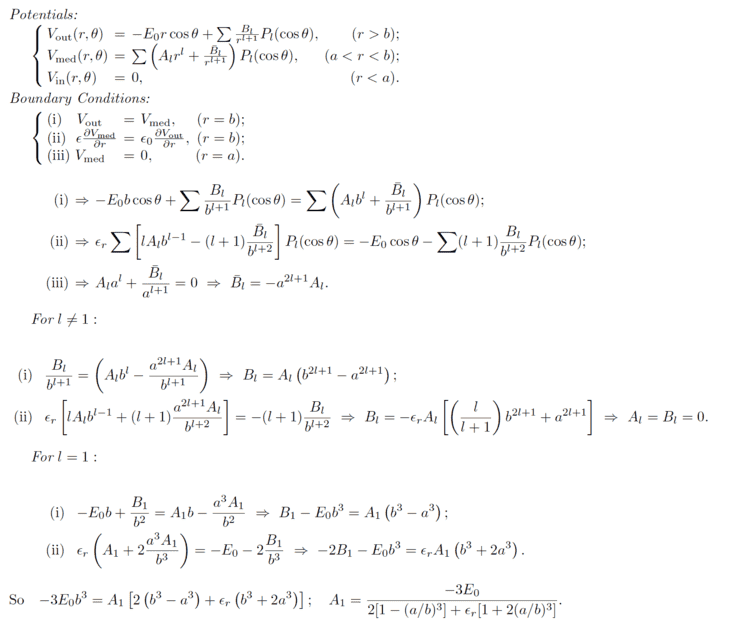
What I am having trouble finding is the dipole moment of the conductor.
I know the formula for dipole moment can be written as p = ∫rσ(r)dA.
Im stuck on how to find σ or if this formula is the right approach.