Understanding 2 Effects of G.R.: Periastron Precession & Pulsation Periods

[Dyatlov]

Hello, after much thought I decided to ask here about the specifics of 2 of the effects of G.R., which are a bit unclear to me.
The scenario is - one pulsar and one neutron star orbiting their barycenter as you can see from the image below (ignore the binary pulsar title of image, it's just what I have found on web).

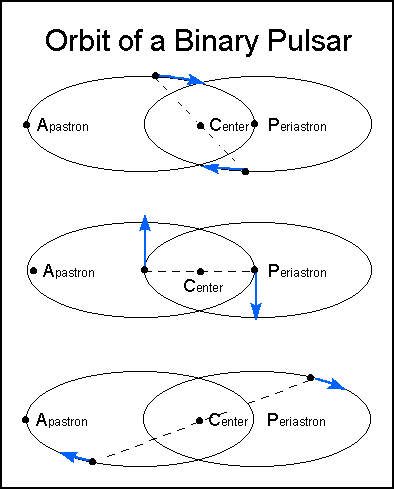
One of the effects of G.R. is that the pulsar's (right orbit) periastron will change over time. The change was measured at 4 degrees each year. It's the same as Mercury with it's change of 43 arc seconds every 100 years of it's perihelion.
Why exactly is that? It's due to the perturbations caused by neutron star on the pulsar's orbit ? Or in case of Mercury, of the other outer planets perturbing it's orbit? I know for Mercury that the Schwarzschild radius/ Mercury-Sun radius is the smallest for the entire solar system, that's why we can see this effect at it's best. It has something to do with ripples in space-time sent outward at c by the Sun and perturbing Mercury's orbit? I would like a link with some in-detail explanation of this effect if it's possible.
Now for the second effect: gravitational redshift. I understand this effect pretty well, but in this scenario (neutron-pulsar system) we are talking about pulsation periods. The change in pulsations can be seen from the formula was ΔPp/ P = [ 1+(Vr/c)/ 1-(Vr/c)]^-1/2 – 1, Vr being the radial velocity.
Now for the actual question: When both objects are at their periastron (so their distance between is at a minimum), the pulsations from the pulsar will be slowed down (from an observer's point of view, which is located outside their gravitational fields). Why is that? Is it because matter pulls time and the presence of the neutron star's gravitational field makes the time go slower from the observer's p.o.v., therefore the pulsations will come at a slower rate from him?
Any help is greatly appreciated.
Thanks in advance.

 

[Mentz114]

Why exactly is that? It's due to the perturbations caused by neutron star on the pulsar's orbit ? Or in case of Mercury, of the other outer planets perturbing it's orbit? I know for Mercury that the Schwarzschild radius/ Mercury-Sun radius is the smallest for the entire solar system, that's why we can see this effect at it's best. It has something to do with ripples in space-time sent outward at c by the Sun and perturbing Mercury's orbit?.

The exact solution for 'elliptical' orbits in the Schwarzschild vacuum is in terms of the Weierstrass $\wp$ function which is modular but has two periods.

The precession just happens - it is difficult to assign a specific cause in view of this solution. Also, the effects of other bodies and the sun's oblateness have been factored into the calculation. The remaining (anomolous) precession is a relativistic effect.

G. V. Kraniotis, S. B. Whitehouse,
Precession of Mercury in General Relativity, the Cosmological Constant and Jacobi's Inversion
problem.
Preprint http://128.84.158.119/abs/astro-ph/0305181v3

 

[Dyatlov]

G. V. Kraniotis, S. B. Whitehouse,
Precession of Mercury in General Relativity, the Cosmological Constant and Jacobi's Inversion
problem.
Preprint http://128.84.158.119/abs/astro-ph/0305181v3

Thanks for the answer. Is this the paper which you are linking? http://arxiv.org/pdf/astro-ph/0305181v4.pdf (yours doesn't work).

 

[Mentz114]

Thanks for the answer. Is this the paper which you are linking? http://arxiv.org/pdf/astro-ph/0305181v4.pdf (yours doesn't work).

Yes. See section 3.1.

[edit]
You could find this relevant to the binary part of your question

Periastron shift in Weyl class spacetimes
Donato Bini, Francesco De Paolis, Andrea Geralico,
Gabriele Ingrosso and Achille Nucita

arXiv:gr-qc/0502062v1 14 Feb 2005

 

[A.T.]

It has something to do with ripples in space-time sent outward at c by the Sun and perturbing Mercury's orbit?

If by ripples you mean gravitational waves, then no. The orbit will precess in a static Schwarzschild space time too, due to the spatial geometry. Simple explanation at bottom here:
http://www.physics.ucla.edu/demoweb..._and_general_relativity/curved_spacetime.html

When both objects are at their periastron (so their distance between is at a minimum), the pulsations from the pulsar will be slowed down (from an observer's point of view, which is located outside their gravitational fields). Why is that?

Gravitational time dilation depends on the gravitational potential difference. When they are closest, their combined masses create the lowest gravitational potential.

 

[Dyatlov]

Thanks for the answer and link. That cleared my first issue.

If by ripples you mean gravitational waves, then no. The orbit will precess in a static Schwarzschild space time too, due to the spatial geometry. Simple explanation at bottom here:
http://www.physics.ucla.edu/demoweb..._and_general_relativity/curved_spacetime.html
Gravitational time dilation depends on the gravitational potential difference. When they are closest, their combined masses create the lowest gravitational potential.

The stronger the gravitational potential is(the closer the clock is to the source of gravitation), the slower time should pass, right?
Well in this scenario you said their combined masses create the lowest gravitational potential therefore the pulse periods should be the fastest not slowest. Did you mean the highest gravitational potential maybe? That would explain my case.

 

[A.T.]

The stronger the gravitational potential is(the closer the clock is to the source of gravitation)

Gravitational potential is lower, closer to the source of gravitation

 

[Dyatlov]

Gravitational potential is lower, closer to the source of gravitation

So clocks that are far from massive bodies (or at higher gravitational potentials) run faster, and clocks close to massive bodies (or at lower gravitational potentials) run slower.
That is why the pulsation periods gets bigger when the two objects are at their periastron.
Thanks a lot for the help.

 

[A.T.]

So clocks that are far from massive bodies (or at higher gravitational potentials) run faster, and clocks close to massive bodies (or at lower gravitational potentials) run slower.

Yes

That is why the pulsation periods gets bigger when the two objects are at their periastron.

Yes, because the gravitational potential goes even lower, with another big mass nearby.