Understanding a 2DOF Problem with One Mass: Help Needed with Setting Up Matrices

[bluechair]

Homework Statement

I need some help with the following problem:

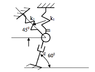
System shown has m=5, k1=100, k2=150, and c=2

Find the natural frequencies, damping ratios, and mode shapes.

The figure of the system has been attached.

2. Known Equations
I know how to find natural frequencies, damping ratios, and mode shapes, my only issue is actually setting up the M, K and C matrices as I have only seen multiple degree of freedom problems with more than one mass, and with all of the springs at 90 degree angles. I am not sure how I am supposed to work this one out.3. Work attempted
I have attempted at setting up this problem twice but I know I am doing it wrong because when I calculate my M^-.5*K*M^-.5 Matrix it does not exist, or it gives me non real numbers as eigenvalues (eg. x=42.6 + or - 17.2603i). Any help setting up the problem would be appreciated.

 

[Valkarie]

Thanks.Homework EquationsM= mass matrix, K= stiffness matrix, C= damping matrixThe Attempt at a SolutionI am not sure how to set up this problem or what matrices I should be using. I have tried twice but both times the eigenvalues are non real numbers so I know I am doing it wrong. Any help would be appreciated. Thanks.