Understanding A Middle Ordinate In Terms Of Geometry

[tomtomtom1]

Hello community

I was hoping someone could help me with the following problem.

I am trying to understand what a middle Ordinate is in terms of geometry (I know it has a versine along a chord).Given the diagram below:-

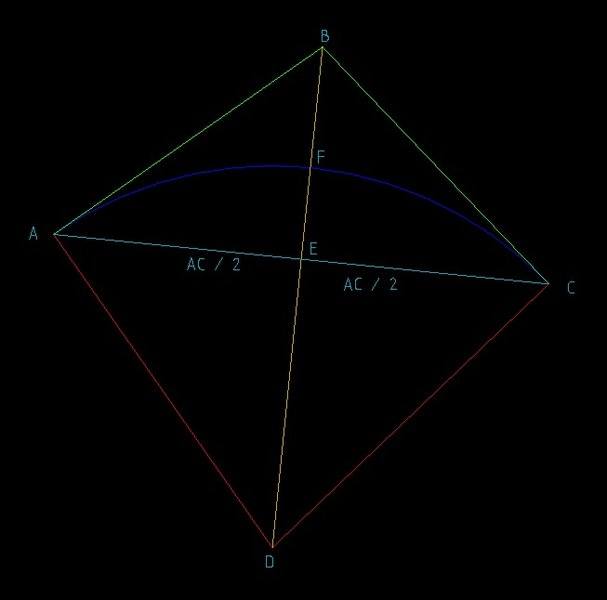
The Blue line is an arc of some radius.

AB & CB are both tangent to the arc and intersect at point B.

AD is 90 Degrees to AB

CB is 90 Degrees to CD


My question is if i drew a line from D to B will that line intersect AC at exactly half its length i.e. at AC/2.

If this is correct then will the length of line EF be its longest when line DB intersects AC at exactly half its length.

I believe that line DB will Always intersect AC at half its distance because AD and CD are the same length making an isosceles triangle.

I also believe that the line EF will be its longest when measured exactly half way along line AC but I cannot prove it.

I was hoping someone could shed some light.

Thank you all.

 

[jambaugh]

Your diagram has some unstated assumptions. Consider the case of a non-square rectangle for example. You can draw an arc "of some radius" through diagonal corners but it won't be symmetric, nor will it be tangent to the sides. Consider the picture below which is clearly a counter example (the brown segments are equal and perpendicular at the corners.

However if you add to your listed assumptions that AB and CB are tangent to the arc then necessarily D is the center of the arc's circle (the lines through AD and CD must pass through the center since they are orthogonal to the tangents at points of tangency.) That makes the sides AD and CD radii and thus equal. That gives you the symmetry by which your conclusion can be shown to be true.

 

[mfb]

@jambaugh: We know that these are tangents.E will always be in the middle of AC, and D is always the center of the circle, which means DF is the radius of the circle. For a constant radius, EF is maximal if DE is minimal, which means the arc between A and C should be as long as possible (but smaller than half the circle to avoid undefined situations or negative lengths).