Understanding Bases of a Vector Space

[NoahsArk]

TL;DR Summary

Need help understanding what a basis of a vector space is

In the book I'm reading, Before Machine Learning, by Jorge Brasil, I'm on the section that introduces bases for vector spaces. The author gives the example of a vector space with two vectors $\vec i$ and $\vec j$ forming the basis where $\vec i = (1,0)$ and $\vec j = (0,1)$ He then says if we want to write a vector $\vec v$ as a linear combination, we can write it as 2 x $\vec i$ + 3 x $\vec j$. I am attaching the picture of this part of the book along with the diagram here:

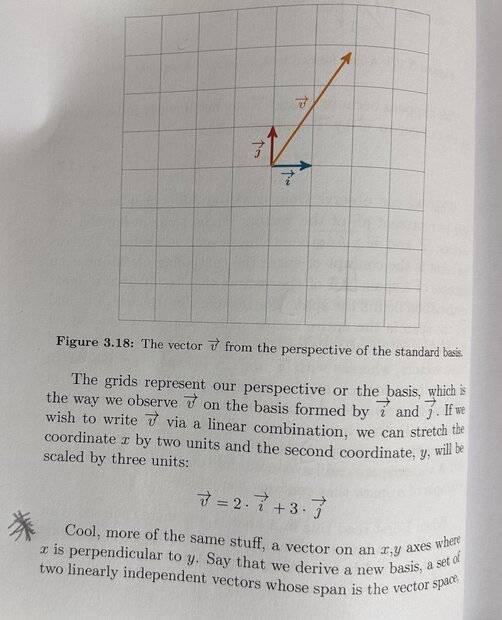
So far this doesn't seem too complicated, but then the author introduces a new basis which is formed by the vectors $\vec w$, and $\vec z$ where $\vec w = (1,0)$ and $\vec z = (1,1)$ He then shows a diagram representing this new basis which I don't understand- I'm pasting a picture of it here:

It appears that he has created a new coordinate plane by slanting the y axis. He has not labeled the coordinates of this plane, though, which is one reason that it's hard to understand. The vectors $\vec w$ and $\vec z$ that he's drawn on it, although he stated that they are supposed to have the coordinates (1,0) and (1,1) respectively, $\vec z$ appears to have the coordinates (0,1) (like $\vec j$) although the author said $\vec z$ is supposed to have coordinates (1,1). How to make sense of this diagram? $\vec v$ on this diagram appears to have coordinates (-4, 3) which I don't think the author intended.

The author then says that if we want to calculate the coordinates of $\vec v$ in this new basis, we will need to find the scalars to multiply $\vec w$ and $\vec z$ by so that when we add these two vectors we get $\vec v$. He then concludes, using the steps in the picture, that the coordinates of $\vec v$ in this basis will be (-1, 3). However, -1 and 3 to me seem not to be coordinates of a vector, but rather two scalars that we need to multiply $\vec w$ and $\vec z$ by to get $\vec v$ which has coordinates (2,3). Please let me know what I'm missing. Thanks.

 

[anuttarasammyak]

They are on the same plane and called orthogonal coordinates and skew coordinates. Orthogonal coordinates are familiar but skew coordinates are useful in some cases e.g. position of atoms in skewed arrangement in crystals. The same point has different (a,b) values in different coordinates and it is OK.

As for distance of two points Pythagoras theorem $d^2=a^2+b^2$ holds for orthogonal coordinates. In skew coordinates
$$d^2=a^2+b^2-2ab \cos\theta$$
where $\theta$ is angle between the axes.

 

[PeroK]

The author then says that if we want to calculate the coordinates of $\vec v$ in this new basis, we will need to find the scalars to multiply $\vec w$ and $\vec z$ by so that when we add these two vectors we get $\vec v$. He then concludes, using the steps in the picture, that the coordinates of $\vec v$ in this basis will be (-1, 3). However, -1 and 3 to me seem not to be coordinates of a vector, but rather two scalars that we need to multiply $\vec w$ and $\vec z$ by to get $\vec v$ which has coordinates (2,3). Please let me know what I'm missing. Thanks.

The first step is to dissocciate the coordinates from the vector. This can be hard to do, because you are so used to thinking of the usual x and y axes and the usual coordinates. For example, we can change the basis simply by swapping the order of the x and y coordinates. We can use $\vec i, \vec j$ to be well-defined "unit" vectors in the x and y directions. Normally, we use these as the basis with the standard coordinates:
$$\vec i = (1, 0)^T, \ \vec j = (0,1)^T$$Note that the equal sign here really means "has these coordinates in the given basis". If we swap the order of the coordinates (give the y-coordinate first), then:
$$\vec i = (0, 1)^T_{yx}, \ \vec j = (1, 0)^T_{yx}$$Note that I've used $_{yx}$ to indicate that these are coordinates in the new basis. Some authors don't do this, but rely on the context to know what basis is being used.

You can choose any pair of vectors as your basis. Let's choose the ones in yiour textbook:
$$\vec w = \vec i = (1,0)^T, \ \vec z = \vec i + \vec j = (1, 1)^T$$Note that these basis vector have those coordinates in the original standard basis.

But, in the new basis (I'll denote this by $wz$ so there is no confusion), these vectors have coordinates:
$$\vec w = (1, 0)^T_{wz}, \ \vec z = (0,1)^T_{wz}$$At this point, you have to be able to reconcile that the coordinates $(0,1)^T_{wz}$ represent the vector $\vec z$ and not the usual $\vec j$.

The next step is to be able to express any other vector in the new $wz$ basis.

 

[Steve4Physics]

Hi @NoahsArk. I can highly recommend this video (by the excellent 3Blue1Brown) which should help: