Understanding Bolted Joints: Shigley's Explanation & Real-Life Testing

[Juanda]

TL;DR Summary

Something does not click in my head about bolted joints.

I'm trying to understand bolted joints better. For reference, this is from Shigley’s.

Conceptually it makes total sense. And it is obviously right especially because it's in THAT book. But when I try to test it myself some contradictions appear and I can't understand what's happening.

First, during the preload process (a→b), the bolt and the clamped components work as springs in series. Is that correct? The same force $F_i$ is applied through them and they have different displacements. Although they are not in the typical physical configuration of springs in series (one spring after the other) I believe they fulfill the definition. Therefore, when applying $F_i$ the clamped parts are being compressed $\delta_m$ and the bolt is being elongated $\delta_b$ (Note that $\delta_m \neq \delta_b$ necessarily since they depend of the stiffness of each of the elements).
Then, during the loading process (b→c) the elements in the joint are working as springs in parallel because they have the same displacement. The displacements being $\Delta \delta_m=\Delta \delta_b$.

I tested the formulas with some nonrealistic numbers to see if I could make sense out of the results. (I'm aware the formulas are only valid as long as gapping does not occur).

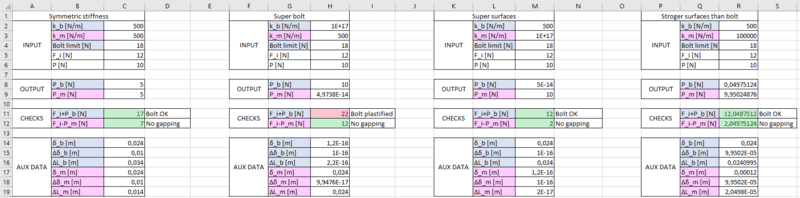
The case with the "super bolt" makes perfect sense. During the preload process with $F_i=12N$ the bolt will need to deform very little $\delta_b \approx 0$ to achieve the preload and the clamped parts will deform much more $\delta_m \neq 0$. Then, when the separation load $P$ is applied, gapping is still very far because the load can be transmitted through the bolt without causing almost any deformation so the clamped force $F_i-P_m \approx F_i$ remains the same and the total load on the bolt is the preload plus the external load $F_i+P_b \approx F_i+P$.

HOWEVER, the case with the "super surfaces" is causing me all kinds of headaches. Now, during the preload process, the bolt will deform significantly compared with the clamped parts which will remain almost undeformed. I have trouble understanding what's happening when the load is applied because I can't wrap my head around the fact that when I apply an external separating load $P$, the tension on the bolt is almost unaffected. It makes sense that the remaining load in the joint is $\approx F_i-P \approx 2N$ but I don't understand why $P$ does not cause an increment in the tension in the bolt. The bolt is what is keeping the clamped parts together so this result feels incredibly counterintuitive to me.

I hope that by understanding these two extreme cases I'll be able to understand all the combinations in between. If there is something not correctly exposed in the post let me know of it and I'll try to be clearer.
Thanks in advance.

PS: By the way, I can share the Excel so you can see the formulas in each cell in case you want to check them but I saw in a different thread that Excel files can contain malware so mods prefer to keep them out of the forum. If you want the file and there is an alternative method to get it to you tell me how and I'll share it.

 

[Baluncore]

I can't wrap my head around the fact that when I apply an external separating load P, the tension on the bolt is almost unaffected.

The separation due to P is small. The bolt is much longer.
That small change in separation of the clamped external faces, is applied over the much greater length of the bolt, so it results in little change in bolt tension.

 

[Juanda]

Yes, in terms of displacements, it makes more sense. Seeing those numbers helped me to understand the case with the extremely rigid bolt. But the rigid clamped surface case is still causing me trouble.

What I believe confuses me is the fact that the rigid clamped parts absorb most of the external load.
The clamped parts only oppose penetration. They keep the bolt in tension because the clamped parts are in compression. So, how is it that when I pull the surfaces with $P$, the force does not travel through the bolt which is the thing working in tension against the external load? How is the compression in the clamped parts helping to resist the external load? The way in which the joint force diminishes makes sense but the fact that the bolt sees almost no change in tension puzzles me extremely.

This by the way is not confusing only to me. I checked a different source (An Introduction to the Design and Behavior of Bolted Joints) which I saw in a thread here from 2015 and it states how other people struggle with this fact as you can see in the third picture. I'm not trying to say it's wrong. I'm saying that although I keep checking the internet and other sources I couldn't make sense of it so far.

The book goes on trying to explain it through an analogy with a car downhill and two persons holding it (The parable of the Red Rolls Royce) but it did not help me to understand it.

In the case where $k_m >> k_b$ (we can even imagine $k_m \rightarrow \infty$) I can keep on loading the joint with $P$ and the bolt will not even see any effect on it until the gap occurs when $P>F_i$. The prediction for when gapping will occur makes sense. The fact the bolt does not see any effect from the load $P$ until it happens breaks me.
Once gapping happens, all the external load will travel through the bolt instead which starts making sense again.

On the other hand, in the case where $k_b>>k_m$ the prediction for gapping being almost impossible makes sense too because the deformation that happened in the clamped parts during the application of the preload $F_i$ will not budge when the external load $P$ is applied. In this case, the load does travel almost entirely through the bolt which also makes sense to me. It is in the previously described scenario that my intuition fails me or even works against me because the math is pretty clear but I am having a very hard time assimilating it.

 

[jrmichler]

In the case where km>>kb (we can even imagine km→∞) I can keep on loading the joint with P and the bolt will not even see any effect on it until the gap occurs when P>Fi. The prediction for when gapping will occur makes sense. The fact the bolt does not see any effect from the load P until it happens breaks me.

It is in the previously described scenario that my intuition fails me or even works against me because the math is pretty clear but I am having a very hard time assimilating it.

Imagine a bolt made from rubber. The bolt stretches, say, one inch when tightened to the proper tension. The bolt is elastic - the tension is proportional to the amount of stretch. The bolt tension holds the parts together. The parts are so stiff that the bolt preload compresses them by, say, 0.0001". If you pull the parts apart with a force slightly less than the bolt tension, they deflect 0.0001". That stretches the bolt 0.0001". The bolt tension changes by the ratio $(1.0000 + 0.0001)/1.0000 = 1.0001$, or almost nothing.

The key to understanding this is to realize that the bolt tension is proportional to the amount of bolt stretch. If the bolt length changes with external load, then the bolt tension is also changing in proportion. If the bolt length does not change, neither does the bolt tension. A perfectly rigid joint will not change dimension with load, so the bolt tension will stay constant.

All of which is why good bolted joint design has a relatively rigid joint and elastic bolt.

 

[Juanda]

I guess I just need time to accept the inner workings of this. The math is clear. Seeing the problem through the lens of deformation makes it more understandable. I'm still struggling but I feel like it is just resistance to demolishing previously built intuitions.

I still want to try to give it one last shot before leaving this slow cooking in the background. I'll draw a free-body diagram with the internal and external forces when I'm back because that's the thing that is confusing me the most. When displacements are considered it makes sense but the force distribution to cause said displacements is where I believe my perception of the problem is flawed.

 

[Juanda]

HOWEVER, the case with the "super surfaces" is causing me all kinds of headaches. Now, during the preload process, the bolt will deform significantly compared with the clamped parts which will remain almost undeformed. I have trouble understanding what's happening when the load is applied because I can't wrap my head around the fact that when I apply an external separating load $P$, the tension on the bolt is almost unaffected. It makes sense that the remaining load in the joint is $\approx F_i-P \approx 2N$ but I don't understand why $P$ does not cause an increment in the tension in the bolt. The bolt is what is keeping the clamped parts together so this result feels incredibly counterintuitive to me.

I think I finally got an intuition about why that happens.
When the external separation force is applied, the tension force on the bolt must increase but simultaneously, the force the clamped parts were doing on the bolt diminishes. The net effect on the bolt depends on the stiffness ratio of the joint.
In the case of the clamped parts being WAY stiffer than the bolt, it is possible to increase the external force until it surpasses the preload so it causes gapping without almost affecting the bolt. At the instant where gapping occurs, all the external force travels exclusively through the bolt but before that, the bolt did not see a significant increment in tension.

Would you say that reasoning is correct? I did not share the FBD for the bolt I mentioned I would do at #5 but I did draw it and it's where it finally clicked in my head.