Understanding Circuits Filter Problem: Steps and Formulas for Solving

[Nubcakes]

I've got this homework problem in a circuits class and I think I understand it but once I get a good ways into it, I kind of run into a dead end. It's kind of hard to explain, so I will just show the problem and my steps toward solving it. Hopefully someone here can point out the flaws in my way

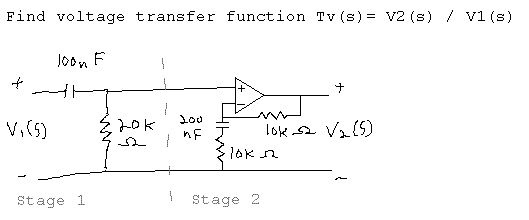
I took the liberty of cutting the circuit into two stages. I am pretty sure you need to do that to solve the problem. First, to find the equation, which I think is the "voltage transfer function", of stage 1 you find the driving point impedance. If you've got coils and/or caps I am pretty sure you need to convert those to the S-Domain.

If I understand how this works correctly; Coils are simply "Ls" and caps are "1/(Cs)". Resistors are simply "R". Using this we can create a formula for stage 1 like this:

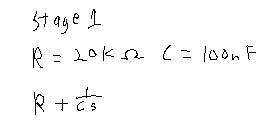
Now, my professor showed very obvious dislike for this form. I believe she converted it to something like this:

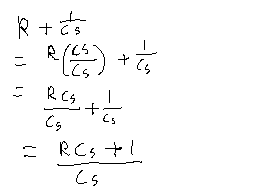
At this point I think you can replace the variables with the units given in the circuit. So, when you replace the variables you get something like this;

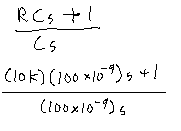
I left the "K" in there to let me know which one is the resistor. Now, I believe this concludes getting the formula for the first stage. Let's move on to the second stage, which I believe is a non-inverting Op-Amp.

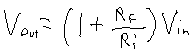
In this case Vin is the result from Stage 1. So once we get the formula for Stage 2, I think we should multiply them together. However, before we can do that, I've got some work to do. Rf is the feed back resistor which can stay the same in this problem. Ri is the input resistor which is not exactly a "resistor" in this case. Since we have a cap and resistor in series it turns out to be similar to what we did in stage 1.

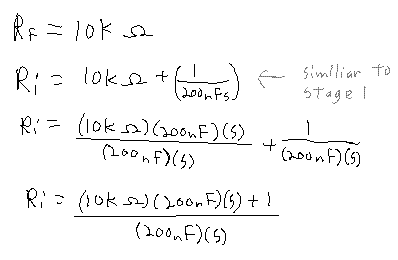
Before I go any further, I found an interesting method for simplifying things with the Op Amp equation.

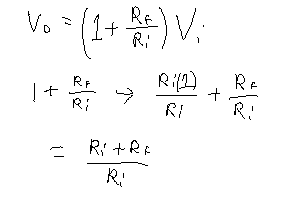
This seems to make things alittle easier. So now we punch in the numbers for everything.

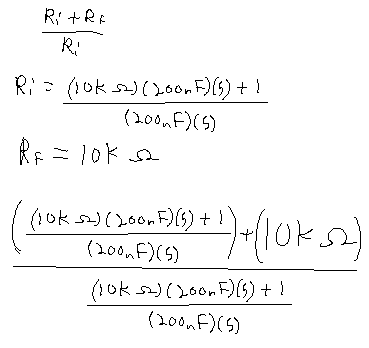
Now that we have an (ugly) equation for Stage 2, we multiply that out with Stage 1's equation.

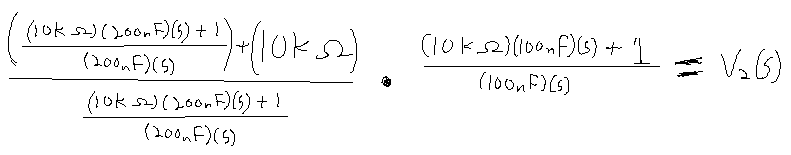
And... this is where I am unsure what to do. I think the result from that function will give V2(s). Since we are not given a value for V1(s) I can't really divide it out. Do I just leave it like that?

The answer in the back of the book is:

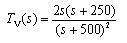
Hopefully this doesn't get deleted for not completely following the format desired by the forum owners

Thanks in advance for any help/hints!~

 

[The Electrician]

For one thing, you've made a numerical error. In the white box labeled Stage1, you have correctly used 20k for the resistor value, but two more boxes down, the 20k became 10k. You should fix that.

Now, you don't want the driving point impedance for the first stage. The driving point impedance is not the same as the transfer function for the first stage.

It's easy to get the transfer function for the first stage; that stage is just a voltage divider. So just calculate the voltage divider output as a function of its input.

In the last white box, you have a complicated expression equated to V2; you should show it equated to V2(s)/V1(S) as in the problem statement.

Finally, after you get the correct transfer function for stage 1, you'll still have a complicated expression. You have to multiply it all out, and then simplify and factor.