- #1
Theman123
- 8
- 0
Hi guys, just before i ask this question i would like to let you know that i am a year 11 student, who has decided to study next years Specialist math (highest level of maths) course early to get a head start as i am nervous for next year(year 12.) :)

and
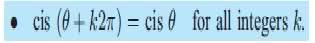
The first one i understand part A and B i have attempted C but am not sure if it the correct method and D i have attempted but have not found an answer, i believe they are related to the second picture. I do not understand how that formula works and need help understanding it, what is the purpose of it?
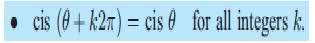 and cisӨ=CosӨ+isinӨ
and cisӨ=CosӨ+isinӨ
z =2cisӨ
A) |z| = 2
arg z = Ө
B)
_
Z = 2(cosӨ-isinӨ)
= 2cosӨ-isinӨ
= 2cos(-Ө)+isin(-Ө)
= 2cis(-Ө)
C) -z = -2cisӨ
= -2(cosӨ+isinӨ)
= -2cosӨ-isinӨ
= -2cosӨ+isin(-Ө)
From here i am stuck, the textbook shows the answer as 2cis(Ө+∏)
D)
_
-Z = -2(cosӨ-isinӨ)
= -2cosӨ+2isin(-Ө)
From here i am stuck again, the textbook shows the answer as 2cis( ∏-Ө)
I believe the answers are used using the formula stated above cis(Ө+k2∏)=cisӨ but i do not understand what it means or why it is used
Please remember that i am self-teaching myself this subject at the moment and will be undertaking it next year for year 12.
Thanks! :)
Homework Statement
and
The first one i understand part A and B i have attempted C but am not sure if it the correct method and D i have attempted but have not found an answer, i believe they are related to the second picture. I do not understand how that formula works and need help understanding it, what is the purpose of it?
Homework Equations
The Attempt at a Solution
z =2cisӨ
A) |z| = 2
arg z = Ө
B)
_
Z = 2(cosӨ-isinӨ)
= 2cosӨ-isinӨ
= 2cos(-Ө)+isin(-Ө)
= 2cis(-Ө)
C) -z = -2cisӨ
= -2(cosӨ+isinӨ)
= -2cosӨ-isinӨ
= -2cosӨ+isin(-Ө)
From here i am stuck, the textbook shows the answer as 2cis(Ө+∏)
D)
_
-Z = -2(cosӨ-isinӨ)
= -2cosӨ+2isin(-Ө)
From here i am stuck again, the textbook shows the answer as 2cis( ∏-Ө)
I believe the answers are used using the formula stated above cis(Ө+k2∏)=cisӨ but i do not understand what it means or why it is used
Please remember that i am self-teaching myself this subject at the moment and will be undertaking it next year for year 12.
Thanks! :)
