member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this,
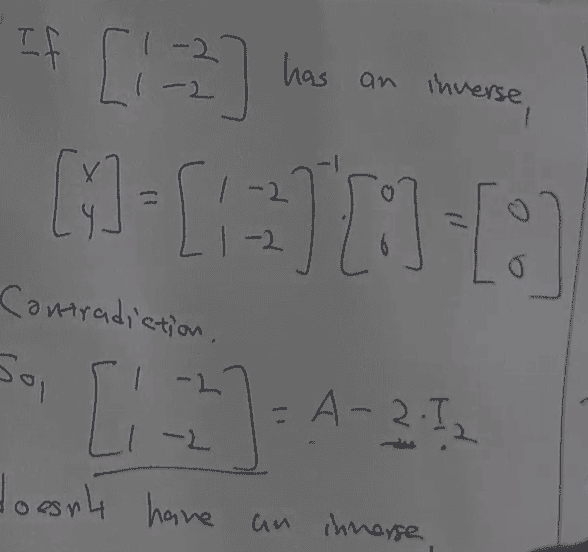
I am confused by the second line. Does someone please know how it can it be true since the matrix dose not have an inverse.
Many thanks!
I am confused by the second line. Does someone please know how it can it be true since the matrix dose not have an inverse.
Many thanks!