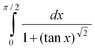Understanding First-Year Calculus Concepts: Integrand and Antiderivative

  • Context: Undergrad 
  • Thread starter Thread starter albema
  • Start date Start date
  • Tags Tags
    Calculus
Click For Summary

Discussion Overview

The discussion revolves around understanding specific calculus concepts, particularly the terms "integrand" and "antiderivative," as well as the concept of "hyperbolicus" related to hyperbolic functions. The scope includes conceptual clarification and definitions relevant to first-year calculus, particularly for engineering students.

Discussion Character

  • Conceptual clarification, Homework-related

Main Points Raised

  • One participant asks for clarification on which terms in an attached image correspond to "integrand" and "antiderivative."
  • Another participant defines the integrand as the function being integrated and the antiderivative as a function whose derivative is the integrand.
  • A participant questions whether "hyperbolicus" refers to "hyperbolic functions" in English.
  • Another participant confirms that "hyperbolis" refers to hyperbolic functions, noting their relation to imaginary cases and suggests further reading for more detailed expressions.

Areas of Agreement / Disagreement

There is some agreement on the definitions of integrand and antiderivative, but the discussion on hyperbolic functions remains less clear, with varying interpretations of the term "hyperbolicus." The overall discussion does not reach a consensus on the latter.

Contextual Notes

The discussion includes assumptions about prior knowledge of calculus and hyperbolic functions, which may not be universally shared among participants.

albema
Messages
8
Reaction score
0
I have 2 questions to ask.

Which is “integrand” and the “antiderivative” on the attached image?

What is “hyperbolicus” (form of trigonometry identities which include e or exponential)?

I am an undergraduate student of engineering, so please tell me the easiest simplest way on this. I see many people here are advance.

Thank you
 

Attachments

  • Sample.JPG
    Sample.JPG
    8.2 KB · Views: 474
Physics news on Phys.org
I'm going to ask what do you think corresponds to each of the terms from the image just in case this is a homework question. Just to define some terms however, the integrand is the function being integrated and the antiderivative is a function whose derivative is the integrand.
 
By "hyperbolicus" do you mean what in English are called the "hyperbolic functions"?
 
The answer to one part is correctly answered by kurdt.Hyperbolis are the hyperbolic functions that take into account the imaginary cases also.More read with the help of google as I am not able to write the expressions here.
 

Similar threads

Intro Math Maths needed to advance my physics understanding
  • · Replies 20 ·
Replies
20
Views
3K
Undergrad Finding equivalent forms prior to integration
  • · Replies 3 ·
Replies
3
Views
4K
Undergrad Grassmannian as smooth manifold
  • · Replies 6 ·
Replies
6
Views
3K
Undergrad Series for Elliptic Integral of the First Kind
  • · Replies 2 ·
Replies
2
Views
2K
High School Changing Perspectives in Math Class: From Memorization to Understanding
  • · Replies 21 ·
Replies
21
Views
4K
Studying What to do in a gap year to prepare for a Physics + Math degree
  • · Replies 15 ·
Replies
15
Views
3K
Should I Take Separate Pre-Calculus and Trigonometry Classes or Combine Them?
  • · Replies 6 ·
Replies
6
Views
6K
Undergrad Bondi ##k##-factor concept from first principles
  • · Replies 41 ·
2
Replies
41
Views
4K
Calculus Suggestion for a proof-based math text book for high school
  • · Replies 3 ·
Replies
3
Views
2K
Is non-rigorous maths more useful for undergraduate physics?
  • · Replies 7 ·
Replies
7
Views
3K