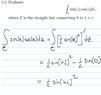- #1
nacho-man
- 171
- 0
Referring to the attached image.
i seem to have forgotten this material and am trying to revise,
how/why does it become $\frac{1}{2}$ $(\sin(z))^2 $' ?
and does the path $C$ that we are given come into play in the solution?
Sorry for the noobness, any help is appreciated!
i seem to have forgotten this material and am trying to revise,
how/why does it become $\frac{1}{2}$ $(\sin(z))^2 $' ?
and does the path $C$ that we are given come into play in the solution?
Sorry for the noobness, any help is appreciated!