- #1
Tosh5457
- 134
- 28
My teacher's notes don't explain this. What are free and bound charges, and why are the H and D field defined like they are?
Tosh5457 said:And how to arrive at the expression:
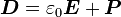
Well, your "definition" has several issues:DrDu said:Dickfore, I think this whole description of polarization in terms of dipole densities of bound charges is very outdated. The polarisation can be defined as [itex] P(t)=\int_{-\infty}^{t}j(t) [/itex] where j(t) is the microscopic charge density. "Macroscopic" values of P or D or epsilon are simply obtained considering the low wavenumber components of its Fourier transform.
Dickfore said:Well, your "definition" has several issues:
- What is your integration variable t?
- As is writen, your formula is dimensionally inconsistent
- The polarization is a vector, whereas charge density is a scalar. So, the formula is also rotationally inconsistent.
DrDu said:t is time, and j is the vector of electric current. So no inconsistency.
Dickfore said:EDIT:
There needs to be a correction to the formula for the bound current density as the curl of magnetization. Namely, it is only valid if the polarization is time-independent.
DrDu said:My point is that it is somewhat artificial to distinguish between bound and free charges. Even relatively localized bonds, like e.g. in silicon form bands which are spread out over the whole solid and this delocalization effects the dielectric function.
Dickfore said:This is wrong. Bands are spread out in energy, not position.
Free charges are particles, such as electrons and protons, that are not bound to atoms and are able to move freely within a material. Bound charges, on the other hand, are particles that are bound to atoms and are unable to move freely.
H and D fields are both used to describe the effects of electric fields on materials. However, the H field only takes into account the free charges, while the D field takes into account both free and bound charges. This means that the D field is a more accurate representation of the electric field in a material.
H and D fields are related through the material's permittivity, which is a measure of how easily electric fields can permeate through a material. The H field is equal to the D field multiplied by the material's permittivity. This means that the H field is affected by both the free and bound charges in a material, while the D field is only affected by the free charges.
Understanding free and bound charges is important in many scientific and technological applications, such as designing electronic devices and studying the behavior of materials under different electric fields. It also helps us better understand the behavior of electricity and electromagnetic waves in different materials.
There are various techniques that can be used to measure free and bound charges in a material, such as capacitance measurements, dielectric spectroscopy, and impedance measurements. These techniques involve applying an electric field to the material and measuring the resulting response, which can then be used to calculate the free and bound charges present.