Understanding Heaps & Deleting Elements

[evinda]

Hi! (Smile)

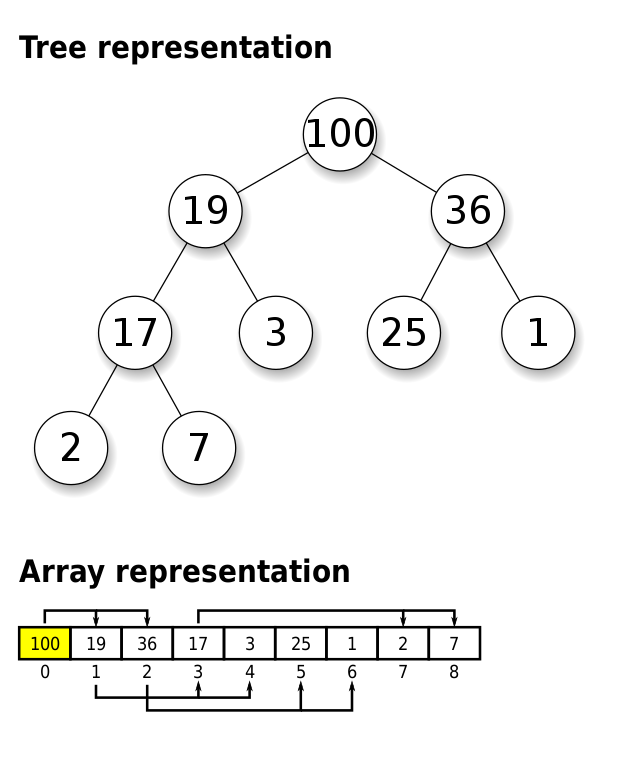
A heap is a complete binary tree $T$. That means that a node of the tree has at most two children and for each nonempty subtree $t$ of $T$ it holds that the key of $t$ is greater than all the keys of the left subtree of $t$ and smaller than all the keys of the right subtree of $t$. Also, it holds that each node has exactly two children except from those from the last level. The nodes from the last level don't have children and the last level has to be filled from the left side without lacks but it hasn't to be complete.

The following is for example a heap, right? (Thinking)

View attachment 3737If we want to delete any element of the heap, do we have to put at its position the last element of the heap and then check if the key of the element we put is greater than the keys of the left subtree and smaller than the keys of the right subtree? (Thinking)

 

[Nono713]

That's not what a heap is as far as I know, you're describing a complete binary search tree. In a heap each node has its children nodes both compare $\leq$ (or $\geq$) their parent node according to some order. For instance this is a heap:

Note that the children of every node are smaller than their parent, but e.g. 19 is smaller than 25 despite being higher up the tree, that's not a problem because they are not in the same subtree.

The Wikipedia article for the binary heap is actually pretty good and even has a description of the insertion and deletion operations, I think it could help if you read through it: Binary heap - Wikipedia, the free encyclopedia.

 

[evinda]

That's not what a heap is as far as I know, you're describing a complete binary search tree. In a heap each node has its children nodes both compare $\leq$ (or $\geq$) their parent node according to some order. For instance this is a heap:
Note that the children of every node are smaller than their parent, but e.g. 19 is smaller than 25 despite being higher up the tree, that's not a problem because they are not in the same subtree.

I see.. (Smile) At the beginning we want to find the element with a specific index $i$ in order to delete it. How can we get access to it? (Thinking)

 

[Nono713]

I see.. (Smile) At the beginning we want to find the element with a specific index $i$ in order to delete it. How can we get access to it? (Thinking)

The heap is generally stored as an array, so accessing an element by its index is just a constant-time lookup into the array. Then its parent and children indices can be found through simple arithmetic. It's written in the Wikipedia article, for what it's worth.

 

[evinda]

The heap is generally stored as an array, so accessing an element by its index is just a constant-time lookup into the array. Then its parent and children indices can be found through simple arithmetic. It's written in the Wikipedia article, for what it's worth.

Suppose that we want to delete the element with index $i$.
Then at the beginning do we have to execute the command:
[m] A=A[n-1][/m]
where [m] n [/m] is the number of elements?
If so how can we delete the element of the $(n-1)^{th}$ position? (Thinking)

 

[Nono713]

Suppose that we want to delete the element with index $i$.
Then at the beginning do we have to execute the command:
[m] A=A[n-1][/m]
where [m] n [/m] is the number of elements?
If so how can we delete the element of the $(n-1)^{th}$ position? (Thinking)

If you simply delete the very last element of a heap, isn't the heap property still satisfied? Which nodes could possibly be affected? Are they?

 

[evinda]

If you simply delete the very last element of a heap, isn't the heap property still satisfied? Which nodes could possibly be affected? Are they?

I haven't understood how we delete the very last element of the heap... (Worried)

 

[Nono713]

I haven't understood how we delete the very last element of the heap... (Worried)

You just remove it from the array and decrease the array's length by 1. Poof, gone. Removing it doesn't affect the heap property of the tree, so it's still a heap after deleting the last element (this isn't true of all nodes, though, of course) and so there's nothing more to be done for that part.

So to delete an arbitrary element (by index) you replace it with the last element of the heap, get rid of the last element of the heap, and then "heapify" the heap by fixing up the tree edges to restore the heap property, which may involve moving nodes around depending on their relative order.

By the way, deleting an arbitrary element is not generally what a heap is for, mainly because you don't often have indices to your heap elements to begin with (and searching in a heap takes linear time in general). Are you sure you really want a heap and not a binary search tree?

 

[evinda]

You just remove it from the array and decrease the array's length by 1. Poof, gone. Removing it doesn't affect the heap property of the tree, so it's still a heap after deleting the last element (this isn't true of all nodes, though, of course) and so there's nothing more to be done for that part.

So to delete an arbitrary element (by index) you replace it with the last element of the heap, get rid of the last element of the heap, and then "heapify" the heap by fixing up the tree edges to restore the heap property, which may involve moving nodes around depending on their relative order.

Aha... (Nod)

By the way, deleting an arbitrary element is not generally what a heap is for, mainly because you don't often have indices to your heap elements to begin with (and searching in a heap takes linear time in general). Are you sure you really want a heap and not a binary search tree?

Yes, I am asked to delete any element of a heap in time $O(\log m)$.So, should the algorithm look like that? (Thinking)

Algorithm(A,i){
   A[i]=A[n];
   n=n-1;
   left=2*i;
   right=2*i+1;
   largest=i;
   if (left<=n and A[left]>A[largest]) largest=left;
   if (right<=n and A[right]>A[largest]) largest=right;
   if (largest!=i){
      swap(A[i],A[largest]);
      Algorithm(A,largest);
   }
}

 

[evinda]

Or do we need also an other condition? (Thinking)
Because if we have for example this heap:

View attachment 3738

after deleting $50$ and heapifying we get this:

View attachment 3739then we swap $A[2]$ with $A[5]$ and then after some changes we get again the same heap as above... (Thinking)
Or does it have to do with the specific example? (Thinking)