Understanding iris electrode and iris doublet (Accelerator physics)

[Wrichik Basu]

TL;DR Summary

I am reading the book "Particle Accelerator Physics" (4th ed.) by Helmut Wiedemann, and facing some problems in understanding the equations describing iris electrode (section 2.2.2) and iris doublet (section 2.2.3).

Iris electrode

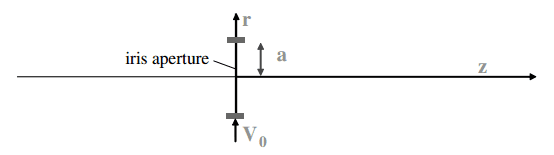
The potential distribution in the vicinity of the iris electrode, denoted by $V(r,z)$ is rotationally symmetric. After some derivations, the author arrives at the following two equations:
$$\begin{align}
E_z &= - V'_0(z)\\
E_r &= \frac{1}{2}V''_0(z)r,
\end{align}$$
where $V_0 (z) \equiv V(r = 0, z)$ and the primes denote derivatives w.r.t. $z$.

Then, using the radial equation of motion $m \ddot{r} = m v^2 r'' = q E_r$, where $v$ and $q$ are respectively the particle velocity and charge, the author defines an integration,
$$\begin{align}
r'_2 - r'_1 &= \dfrac{q}{mv^2} \int_{z_1}^{z_2} E_r ~ \mathrm{d}z \nonumber \\[2em]
&= - \dfrac{q}{2mv^2} \int_{z_1}^{z_2} r \dfrac{\partial E_z}{\partial z} \mathrm{d}z \label{eq:integration}
\end{align}$$
(The second step above stems from the fact that $\nabla \cdot \mathbf{E} = 0$)

In the thin lens approximation ($r = \mathrm{const.}$ and $v = \mathrm{const.}$, see diagram above), $\mathrm{Eqn. \eqref{eq:integration}}$ becomes
$$\begin{equation}
r'_2 - r'_1 = - \dfrac{q~r_1}{2mv^2} (E_2 - E_1) \label{eq:2}
\end{equation}
$$
Substituting $\frac{1}{2} m v^2 = q V_0$ and $E = -V'$, $\mathrm{Eqn.}~\eqref{eq:2}$ becomes
$$
r_2' - r_1' = \dfrac{r_1}{4} \dfrac{V_2' - V_1'}{V_0},
$$
and the focal length of the iris electrode is
$$\begin{equation}
\frac{1}{f} = \dfrac{V_2' - V_1'}{4V_0}, \label{eq:focal_length}
\end{equation}$$
and the transformation matrix finally becomes
$$\begin{equation}
\mathcal{M}_\mathrm{iris} = \begin{pmatrix}
1 & 0\\
\dfrac{V_2' - V_1'}{V_0} & 1
\end{pmatrix}. \label{eq:trans_mat_1}
\end{equation}$$
Questions:

1. This is the first time the author mentions the transformation matrix. What is the significance of this matrix?​

2. How is the transformation matrix constructed from the focal length?​

Iris doublet

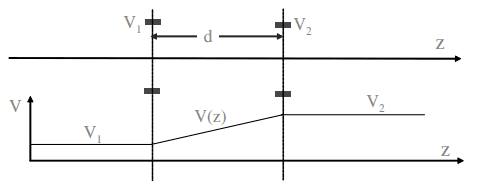
Let me go ahead and simply quote the author:

The transformation matrices for both iris electrodes are,
$$\begin{align}
\mathcal{M}_1 &= \begin{pmatrix}
1 & 0\\
\dfrac{V_2 - V_1}{4dV_1} & 1
\end{pmatrix} \label{eq:trans_mat_iris1}\, \mathrm{and} \\[2em]
\mathcal{M}_2 &= \begin{pmatrix}
1 & 0\\
\dfrac{V_2 - V_1}{4dV_2} & 1
\end{pmatrix}. \label{eq:trans_mat_iris2}
\end{align}$$
The transformation matrix for the drift space between the electrodes can be derived from the particle trajectory
$$\begin{align}
r(z) &= r_1 + \int _0^z r'(\bar{z}) ~ \mathrm{d}\bar{z} \label{eq:some1}\\[2em]
&= r_1 + \int _0^z \mathrm{d}\bar{z} ~ \dfrac{r' ~ p_1}{p_1 + \Delta p(\bar{z})} \label{eq:some2}
\end{align}$$
The particle momentum varies between the electrodes from $p_1 = \sqrt{2mE_\mathrm{kin}}$ to $p_1 + \Delta p(\bar{z}) = \sqrt{2m \left(E_\mathrm{kin} + q \dfrac{V_2 - V_1}{d}z \right)}$ and the integral becomes
$$\begin{equation}
\int_0^d \dfrac{\mathrm{d}\bar{z}}{\sqrt{1 + \frac{V_2 - V_1}{E_\mathrm{kin}d}\bar{z}}} = \dfrac{2d \sqrt{V_1}}{\sqrt{V_2} + \sqrt{V_1}}. \label{eq:some3}
\end{equation}$$
The particle trajectory at the location of the second electrode is $r(d) = r_2 = r_1 + \dfrac{2d \sqrt{V_1}}{\sqrt{V_2} + \sqrt{V_1}}r'_1$ and its derivative $r'_2 = r'_1 \sqrt{V_1}/\sqrt{V_2}$ from which we can deduce the transformation matrix
$$\begin{equation}
\mathcal{M}_d = \begin{pmatrix}
1 & \dfrac{2d \sqrt{V_1}}{\sqrt{V_2} + \sqrt{V_1}}\\[1.5em]
0 & \dfrac{\sqrt{V_1}}{\sqrt{V_2}}
\end{pmatrix} \label{eq:trans_mat_4}
\end{equation}$$

Questions:

3. How does the transformation matrix change from that in $\mathrm{Eqn.}~\eqref{eq:trans_mat_1}$ to $\mathrm{Eqn.}~\eqref{eq:trans_mat_iris1}?$ How do the primes change to unprimed variables, and how does the $d$ come in the denominator?​

4. How do we go from $\mathrm{Eqn.}~\eqref{eq:some1}$ to $\mathrm{Eqn.}~\eqref{eq:some2}?$​

5. How do we get the transformation matrix in $\mathrm{Eqn.}~\eqref{eq:trans_mat_4}?$​