Understanding Potential Difference in a Cubic Circuit

[V0ODO0CH1LD]

Homework Statement

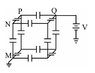
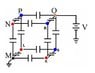
A potential electrostatic difference is stablished between points M and Q in the cubic circuit of identical capacitors shown in the image. What is the potential difference between points N and P?

Homework Equations

The Attempt at a Solution

I tried opening up the cube to make it look like something that I am used to, but it still looked confusing.

 

[mfb]

There are two unnamed points equivalent to N, and two unnamed points equivalent to P. You can add (imaginary) connections between them, this allows to draw a simple, equivalent planar diagram.

 

[V0ODO0CH1LD]

There are two unnamed points equivalent to N, and two unnamed points equivalent to P. You can add (imaginary) connections between them, this allows to draw a simple, equivalent planar diagram.

Would it be correct to assume that whatever current I have flowing into M it gets split up in three? And then in two at the next node? Reuniting at the end to deliver the same current to node Q?

I tried to draw an equivalent diagram, but I can't get it to look right.. I think there's something I am missing.

 

[mfb]

Would it be correct to assume that whatever current I have flowing into M it gets split up in three? And then in two at the next node? Reuniting at the end to deliver the same current to node Q?

Right. And you can draw this as planar graph as well.

 

[V0ODO0CH1LD]

Right. And you can draw this as planar graph as well.

I struggled a lot with it.. Than I came across this article that explained a similar problem but with resistors!

In the article, it said that since the first three nodes from the source of potential difference have the same current going though them. I can assume they are somehow equivalent points. And by using the same assumptions with the remaining nodes you can arrive at a schematic where you have two sets of three capacitors in parallel in series with six capacitors in parallel. Like M--(3 parallel)---(6 parallel)---(3 parallel)--Q.

The thing is, I don't get how you could arrive at this. How can I just say that those three first nodes could be represented by one?

Also trying to flatten the cube will get you nowhere. I tried all possibilities.. Either you have to understand the assumption above or I am really missing something. Because I just couldn't do it..

 

[ehild]

The problem of cube of resistors was discussed in Physicsforums several times. Try to follow this thread: https://www.physicsforums.com/showthread.php?t=557461

The method of solution is based on symmetry. (See the thread from Post #6) Equivalent points are at the same potential. Points on same potential can be connected with a wire, it changes nothing in the electric circuit. The points connected with a wire of zero resistance represent a single node.

ehild

 

[V0ODO0CH1LD]

The problem of cube of resistors was discussed in Physicsforums several times. Try to follow this thread: https://www.physicsforums.com/showthread.php?t=557461

The method of solution is based on symmetry. (See the thread from Post #6) Equivalent points are at the same potential. Points on same potential can be connected with a wire, it changes nothing in the electric circuit. The points connected with a wire of zero resistance represent a single node.

ehild

Thanks! I was also wondering something else: is the voltage across the whole cube the same? If I measured the electric potential difference between any two points will they all give back the same value? Because I was thinking; if I measured the voltage from point M to point N and from point N to point P, they would differ. Because I have the same resistance but half the current, and by Ohm's law V = IR, the voltage of between M and N would be twice the voltage between N and P. Is that correct?

 

[ehild]

I drew the equivalent points by coloured dots. The voltage is the same between identical pairs: between the black dot and the red ones, (that is between M and N , M and K, M and L). It is the same also between the blue ones and the orange one: PQ, RQ, SQ. But it is different for the other pairs.
The voltage between M and N is not the same as the voltage between N and P. It is a bit easier to follow the potential of the nods. M is at zero potential and Q is at V potential. The potential increases with the same amount from M to N, from M to K and from M to L, and the same is the increase from P to Q, from R to Q and from S to Q. But you get different change of potential from N to P, N -->R, L-->S, L-->P, K-->R, K-->S.

ehild

 

[V0ODO0CH1LD]

Okay, but I am still confused as to why the potential difference is different from:
N --> P, N -->R, L-->S, L-->P, K-->R, K-->S.

If I had three amperes flowing into M. Would't that current split into three currents of one ampere each flowing towards N, L and K? Then at those nodes they would split yet again into two currents of 1/2 ampere? So that you would have flowing into P 1/2 A from N and 1/2 A from L? And into S; 1/2 A from K and 1/2 A from L?

 

[CWatters]

Okay, but I am still confused as to why the potential difference is different from:
N --> P, N -->R, L-->S, L-->P, K-->R, K-->S.

I think you missunderstood what he said. He meant...

Vblack to Vred = Vblue to orange <> Vred to Vblue

There are three caps between black and red and between blue and orange but six caps between red and blue.

 

[ehild]

Okay, but I am still confused as to why the potential difference is different from:
N --> P, N -->R, L-->S, L-->P, K-->R, K-->S.

These are all equal, but different from V_MN (half of it).

ehild