Understanding Proper Time Concept in Relativity: Clock Readings and Observers

[Volcano]

Hi,

I hope asking in right forum.

I'm trying to understand proper time concept but I'm afraid couldn't understand the reason of answer for below question.

"Figure 37-18 shows two clocks in stationary frame S (they are syncronized in that frame) and one clock in moving frame S'. Clocks C₁ and C₁' read zero when they pass each other. When clock C₁' and C₂ pass each other,

(a) Which clock has the smaller reading

and

(b) which clock measures a proper time?
"

What I couldn't understand here is, how can I determine the observer in this type of question. I'm sure those clocks giving the hints about events but how? And yes, (a) and (b) asking the same thing. Proper time always smaller.

 

[Ibix]

I don't think the question is well posed. A clock always measures its own proper time, by definition (the root of the word "proper" is Latin, relating to "your own", like property, I believe). So all the clocks show a proper time - just not the same proper time...

I would guess that the question wants to know about the proper time relating to the interval between the events "C₁ and C'₁ are at the same place" and "C₂ and C'₁ are at the same place". In that case, can you work out which clock shows that proper time?

 

[PeterDonis]

What I couldn't understand here is, how can I determine the observer in this type of question.

You don't really need to; at least, not if you mean an "observer" separate from the clocks themselves. See below.

I'm sure those clocks giving the hints about events but how?

Do you know how to draw a spacetime diagram? If so, that's how. If not, I strongly recommend learning how. It makes analyzing relativity problems a *lot* easier.

Even in the absence of a diagram, it should be evident that there are only two events of interest in the problem as described. Can you see what they are? (Remember, an "event" is a particular happening that occurs at a point in space at an instant of time. For example, when two objects in relative motion pass each other, that's an event.) There is a third event that you can construct to help get the answer to question (a); it's an event of the form "a particular clock has a particular reading", which only requires a single object, the clock, to define.

And yes, (a) and (b) asking the same thing.

No, they aren't. As Ibix pointed out, every clock measures its own proper time. There is no one universal proper time; there is only the individual proper time of each object in its particular state of motion. So question (b) isn't really a well-posed question at all.

Question (a) is well-posed, however (and if I were writing the problem, it's the only question I would have included). I suspect by "proper time" in (b) they meant the proper time of the moving clock, C1', but they didn't phrase it very well.

 

[WannabeNewton]

The proper time asked for by the question is the time as measured on a clock that physically passes between two specific events which are of relevance to the problem. It is akin to asking for the proper time between two given events as measured on a clock carried by an observer whose worldline passes through the two events.

 

[Volcano]

Thanks for your help. Unfortunatly don't know drawing a diagram in this subject. And.. :( Trying to understand.. The events happening(space coordinates) in the stationary frame(S) is it? And the observer is in moving frame(?!). Are these true?

By the way, this question is from Fundamentals Of Physics.

 

[Popper]

I'm trying to understand proper time concept but I'm afraid couldn't understand the reason of answer for below question.

The concept of proper time is really very simple.

First, let’s consider first how it’s used in special relativity (SR). SR is concerned with inertial frames in flat spacetime. The proper time between two events is the time recorded on a clock that is moving at constant velocity and is present at both events, i.e. the (straight) worldline of the clock passes through each event.

This can be extended to general relativity as follows; the proper time between two events along a particular worldline is the time recorded on a clock which moves on the worldline between the two events.

Note: proper time cannot be defined between two events which do not have a timelike worldline connecting them.

 

[Volcano]

Thank you. Then in this question C1' is the clock which present at both events. Is this what you mean?

 

[Popper]

Thank you. Then in this question C1' is the clock which present at both events. Is this what you mean?

I didn't read your example. I've been having problems seeing lately. It's very hard for me to read the screen. I have a cataract in my left eye so everything is blurry and hard to read. I can't get glasses until a while after the surgery I'm having on it in July.

My appologies.

 

[Volcano]

I hope you'll get better soon. July is not so far. Thank you again. Regards

 

[Popper]

I hope you'll get better soon. July is not so far. Thank you again. Regards

Thank you. That was very kind of you to say. It's a pain in the butt now. Not too long ago I bought myself a 60" flat screen LCD High Def LG TV. It's awesome but I'm looking at it through one clear eye and one blurry eye. :(

 

[PeterDonis]

The events happening(space coordinates) in the stationary frame(S) is it?

Events happen in every frame, but they can have different coordinates in different frames.

And the observer is in moving frame(?!).

Observers are present in all frames too, but they will only be at rest in one particular frame. Which frame depends on which observer. If it's the clock C1', or an observer moving along with it, then that observer is at rest in the moving frame in this scenario.

 

[Volcano]

Thank you. Yes I agree. There are events and observers for each frame but the reason of asking the question is, I am having difficulty to determining the frame of events (and observers). How do I know in which frame the events happening in this example question?

.. If it's the clock C1' ..

If this is not an assumption can you tell me how can I detect?

 

[Mentz114]

Thank you. Yes I agree. There are events and observers for each frame but the reason of asking the question is, I am having difficulty to determining the frame of events (and observers). How do I know in which frame the events happening in this example question?If this is not an assumption can you tell me how can I detect?

All events happen in all frames. Proper time is frame independent so it makes no difference which frame ( ie which coordinate basis ) is used for this question.

 

[PeterDonis]

How do I know in which frame the events happening in this example question?

It's not a question of which frame the events are happening in; it's a question of which frame you choose for analyzing the problem. The question itself doesn't tell you that; you have to choose a frame that you think will help you analyze the problem.

If this is not an assumption can you tell me how can I detect?

It's not a question of detecting anything. There is certainly a frame in which the clock C1' is at rest; all I was saying is that you can, if you like, choose that frame, which you are calling the "moving frame", to analyze the problem, and if you do, the "observer" will be at rest in that frame.

 

[ghwellsjr]

Hi,

I hope asking in right forum.

I'm trying to understand proper time concept but I'm afraid couldn't understand the reason of answer for below question.

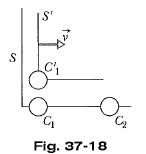
"Figure 37-18 shows two clocks in stationary frame S (they are syncronized in that frame) and one clock in moving frame S'. Clocks C₁ and C₁' read zero when they pass each other. When clock C₁' and C₂ pass each other,

(a) Which clock has the smaller reading

and

(b) which clock measures a proper time?
"

What I couldn't understand here is, how can I determine the observer in this type of question. I'm sure those clocks giving the hints about events but how? And yes, (a) and (b) asking the same thing. Proper time always smaller.

Let's start with the S' frame in which the C'₁ clock is at rest at the spatial origin. I have drawn a spacetime diagram to represent this situation:

I'm assuming that the speed of light is one foot per nanosecond and I draw dots at each tick of a clock. Each dot represents an event with its own coordinates in this Inertial Reference Frame (IRF). Does this make sense to you?

Now we want to see what the events for this clock looks like in the S frame. To do that, we have to realize that the S frame is moving to the left with respect to the S' frame and we plug the numbers for each event into the Lorentz Transformation and make a new IRF diagram:

Now we can add in the other two clocks that are at rest in the S frame:

I have labeled a couple tick marks for each clock with colors matching the colors of the worldlines for each clock. You can see that when the C'₁ reaches the C₂ clock, it has less time on it, 8 nsecs compared to 10 nsecs.

As has been pointed out by others in this thread, each clock keeps track of its own Proper Time. The grid lines mark off the Coordinate Time for each IRF which matches the Proper Time for clocks that have been synchronized to the Coordinate Time and remain stationary in the IRF. This would apply to clocks C₁ and C₂ in the last IRF. We don't normally refer to the Proper Time on such clocks since they match the Coordinate Time and are usually included just to visualize the Coordinate Time. I'm guessing this is the point of the problem and so the answer they are seeking is that it is the C'₁ clock that is measuring the smaller Proper Time when it reaches the C₂ clock but technically, all clocks are measuring Proper Time.

Your statement that Proper Time is always smaller isn't complete--smaller than what? The correct answer is that the Proper Time of a moving clock in an IRF is smaller than the Coordinate Time of the IRF (provided that the clock was synchronized to zero at the Coordinate Time of zero). Note that this is true for the entire trip of the C'₁ clock, even when it is not colocated with another clock. There is always a Coordinate Time (and Location) for the moving clock that you can compare its Proper Time to.

As far as observers go, we normally place observers at rest at the spatial origin of an IRF which means that the C'₁ clock would represent an observer in the first IRF diagram and the C₁ clock would represent an observer in the last IRF diagram. The problem didn't mention any observers. What is your interest in observers?

 

[pervect]

Hi,

I hope asking in right forum.

I'm trying to understand proper time concept but I'm afraid couldn't understand the reason of answer for below question.

"Figure 37-18 shows two clocks in stationary frame S (they are syncronized in that frame) and one clock in moving frame S'. Clocks C₁ and C₁' read zero when they pass each other. When clock C₁' and C₂ pass each other,

(a) Which clock has the smaller reading

and

(b) which clock measures a proper time?
"

<image snipped>

What I couldn't understand here is, how can I determine the observer in this type of question. I'm sure those clocks giving the hints about events but how? And yes, (a) and (b) asking the same thing. Proper time always smaller.

Emphasis added.

It's easy. A direct measurement of proper time does not require any notion of synchronizing two different clocks. This is because proper time can be directly measured using only one clock.

In your example, which measurement involves only one clock? (This measurement will be a measurement of proper time).

Which measurement involves two clocks which much be synchronized? (This measurement will NOT be a measurement of proper time).