zenterix
- 774
- 84
- TL;DR Summary
- I'd like to understand a section of a book I am reading ("Introduction to Special Relativity" by Resnick).
I will create a series of posts that go through snippets of the section "relativistic kinematics" of the book and try to interpret the content in my own words and perform certain calculations that were left for the reader to do.
In a previous post, I investigated a wrong way to synchronize clocks in a single inertial reference frame.
Here is a correct way
A few observations
1) These methods all place clocks at specific locations and synchronize them using signals (namely, light). This is a practical matter: if we could send a signal from one location to another instantly, ie with an infinite speed, then all clocks could be synchronized at the same instant. We don't have such an infinite-speed signal, however.
2) Given that all clocks in a reference frame can be synchronized in, we can judge time order of events in that frame. The time of an event is measured by the clock whose location coincides with that of the event.
3) Events occurring at two different places in the frame are called simultaneous when the clocks at their respective locations record the same time for them.
Now, the next big question is: suppose one inertial observer does find that two separated events are simultaneous; will these same events be measured as simultaneous by an observer on another inertial frame moving with speed ##v## with respect to the first?
An example to understand relativity of simultaneity
We have two reference frames, S and S', having a non-zero relative velocity.
Two events occur in each frame and leave a mark at that position in space (the book uses as an example a lightning bolt or an explosion of dynamite as an event).
Pictorially,
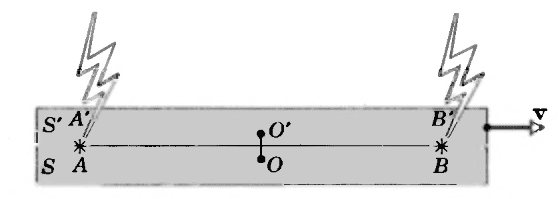
The origin of both frames when the events happen is this midway point. Frame S' is moving to the right relative to frame S with velocity ##\vec{v}##.
Implicit here seems to be that we have two observers, and each one is at the origin of one of the two frames. Thus, observer S' (located at the origin of frame S') is moving with velocity ##v## relative to observer S. Is this so?
The book then shows a few pictures from the point of view of observer S.
Here we see the light waves from event B arriving at observer S' (who has moved a bit to the right)
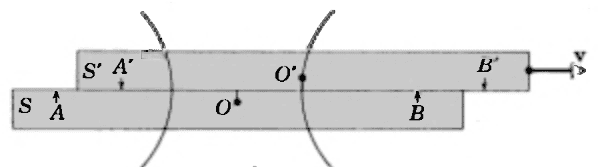 and here, at a later time, we see the waves from both events arriving at observer S.
and here, at a later time, we see the waves from both events arriving at observer S.
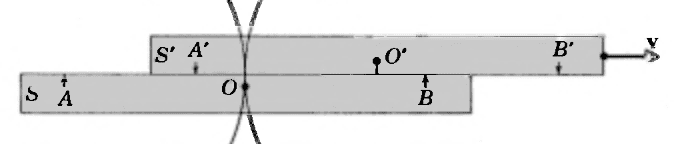
at an even later time, the light from event A arrives at observer S'
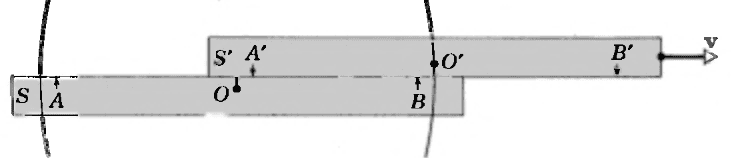
One thing that I find confusing here is that ##A'## and ##B'## are moving relative to S and at rest relative to S'.
My impression is that the explosions (or lightning bolts) occurred at some specific location in spacetime that is independent of the frame we are using to give that location coordinates. I would have thought that frame B would be moving away from A and A' and moving towards B and B' (before passing these locations and then moving away from them).
After all, the light signals originated at A and B in frame S (which in frame S' are points with velocities ##-\vec{v}##.
Okay, moving on.
The signals arrive at 0 at the same time (as measured from the clock at 0) and so A and B are simultaneous in frame S.
Why is the book calling the events BB' and AA' now?
I get that the light signals do not arrive at the same time at the S'-observer. In other words, they arrive at the S'-observer at different times (as measured by frame S' clock at 0' when the signals arrive).
But this BB' thing and the moving B' is bothering me.
Here is a correct way
An alternative would beLet us imagine an observer with a light source that can be turned on and off (e.g. a flash bulb) at each clock, ##A## and ##B##. Let the measured distance betweeen the clocks (and observers) be ##L##.
The agreed-upon procedure for synchronization then is that A will turn on this light source when his clock reads ##t=0## and observer B will set his clock to ##t=L/c## the instant he receives the signal. This accounts for the transmission time and synchronizes the clocks in a consistent way.
A method equivalent to the above is to put a light source at the exact midpoint of the straight line connecting A and B and inform each observer to put his clock at ##t=0## when the turned-on light signal reaches him. The light will take an equal amount of time to reach A and B from the midpoint, so tha this procedure does indeed synchronize the clocks.
A few observations
1) These methods all place clocks at specific locations and synchronize them using signals (namely, light). This is a practical matter: if we could send a signal from one location to another instantly, ie with an infinite speed, then all clocks could be synchronized at the same instant. We don't have such an infinite-speed signal, however.
2) Given that all clocks in a reference frame can be synchronized in, we can judge time order of events in that frame. The time of an event is measured by the clock whose location coincides with that of the event.
3) Events occurring at two different places in the frame are called simultaneous when the clocks at their respective locations record the same time for them.
Now, the next big question is: suppose one inertial observer does find that two separated events are simultaneous; will these same events be measured as simultaneous by an observer on another inertial frame moving with speed ##v## with respect to the first?
An example to understand relativity of simultaneity
We have two reference frames, S and S', having a non-zero relative velocity.
Two events occur in each frame and leave a mark at that position in space (the book uses as an example a lightning bolt or an explosion of dynamite as an event).
Assume that afterwards, by measurements, each inertial observer finds that he was located exactly at the midpoint of the marks which were left on his reference frame.
Pictorially,
The origin of both frames when the events happen is this midway point. Frame S' is moving to the right relative to frame S with velocity ##\vec{v}##.
Implicit here seems to be that we have two observers, and each one is at the origin of one of the two frames. Thus, observer S' (located at the origin of frame S') is moving with velocity ##v## relative to observer S. Is this so?
Ok.Because each observer knows he was at the midpoint of the mark left by these events, he will conclude that they were simultaneous if the light signals from them arrive simultaneously at his clock. If, on the other hand, one signal arrives before the other, he will conclude that one event preceded the other. Since each observer has a synchronized set of clocks, he can conclude either that the clocks at the marks read the same time when the marks were made (simultaneous case) or that they read different times (non-simultaneous case).
I suppose this depends on the velocity of each frame relative to the locations of the events?Many different possibilities exist in principle as to what the measurements might show.
This assumption contains the assumption then that frame S is at rest relative to the event locations.Let us suppose, for sake of argument, that the S-observer finds that the lightning bolts struck simultaneously.
The book then shows a few pictures from the point of view of observer S.
Here we see the light waves from event B arriving at observer S' (who has moved a bit to the right)
at an even later time, the light from event A arrives at observer S'
One thing that I find confusing here is that ##A'## and ##B'## are moving relative to S and at rest relative to S'.
My impression is that the explosions (or lightning bolts) occurred at some specific location in spacetime that is independent of the frame we are using to give that location coordinates. I would have thought that frame B would be moving away from A and A' and moving towards B and B' (before passing these locations and then moving away from them).
After all, the light signals originated at A and B in frame S (which in frame S' are points with velocities ##-\vec{v}##.
Okay, moving on.
The signals arrive at 0 at the same time (as measured from the clock at 0) and so A and B are simultaneous in frame S.
The S'-observer, however, finds that event BB' precedes event AA' in time; they are not simultaneous to him.
Why is the book calling the events BB' and AA' now?
I get that the light signals do not arrive at the same time at the S'-observer. In other words, they arrive at the S'-observer at different times (as measured by frame S' clock at 0' when the signals arrive).
But this BB' thing and the moving B' is bothering me.
Last edited: