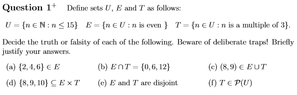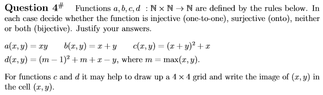Plonker1
- 3
- 0
View attachment 6500
View attachment 6501
View attachment 6502
View attachment 6503
I'm having issues with the first four questions and have uploaded them. My attempts are shown below.
1.
a) True, all elements of E are even
b) False, 0 is not a multiple of 3
c) True, 8 is even and 9 is a multiple of 3
d) No idea
e) False, 6 is an element of E and T
f) No idea
2.
a) You can see my drawing attempt on imgur, sorry for the messiness (ed's note: see below). The parts meant to be coloured in are in black.
b) This claim is false
c) I drew up another graph that I guessed proves it is false. Am I correct?
3&4 I have no idea how to do.
Thank you so much for any help,
A struggling student.
View attachment 6505
View attachment 6504
View attachment 6501
View attachment 6502
View attachment 6503
I'm having issues with the first four questions and have uploaded them. My attempts are shown below.
1.
a) True, all elements of E are even
b) False, 0 is not a multiple of 3
c) True, 8 is even and 9 is a multiple of 3
d) No idea
e) False, 6 is an element of E and T
f) No idea
2.
a) You can see my drawing attempt on imgur, sorry for the messiness (ed's note: see below). The parts meant to be coloured in are in black.
b) This claim is false
c) I drew up another graph that I guessed proves it is false. Am I correct?
3&4 I have no idea how to do.
Thank you so much for any help,
A struggling student.
View attachment 6505
View attachment 6504
Attachments
Last edited by a moderator: