Understanding Shear Force: How to Calculate and Interpret Shear Force Diagrams

[tomtomtom1]

TL;DR Summary

Understanding Shear Force

Hello all

I was hoping some could shed some light on the idea of shear force on members.

I have the following simply supported beam:-

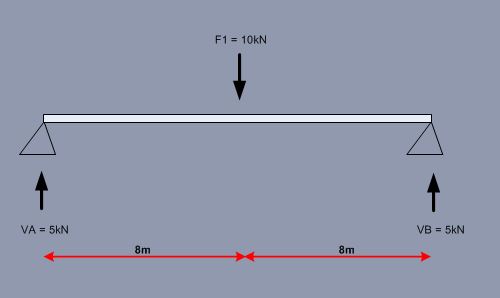
Considering only the left of the beam to just to the right of F1; my gut instinct would be to say that the shear force or failure is greatest at the following location:-

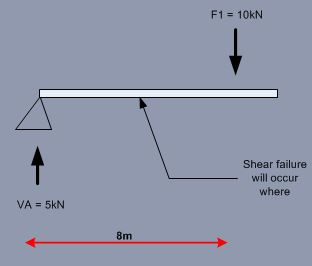The reason I state this is because my understanding of Shear force is that there is a force acting in one direction on a member and another force acting in the opposite direction - so for me the above diagram is correct but I have been told that this is incorrect and the greatest shear force is taken from the shear force diagram and would be the greatest difference between all the vertical forces as shown below:-

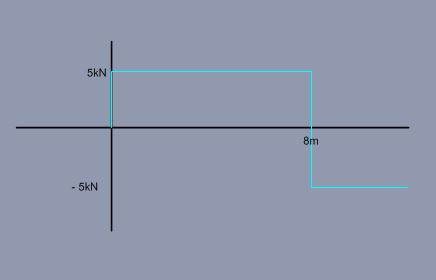The greatest difference in shear is at the 8m point - so would I interpret this at where I will likely get shear failure?

Can anyone explain shear, how to calculate the shear force and interpreting a shear force diagram?

Thank you.

 

[256bits]

Hello @tomtomtom1
You need to do several problems to get a feel for it.

What you have to do is take the beam, do a cut in it, and then do a FBD ( free body diagram ) of the cut beam, determining the forces on the cut face.
Say you cut the beam 1.4 way from the left end.
There is a force of 5 kN in the y- direction at point 0.
What forces would have to act on the face to keep the cut beam in static equilibrium?

 

[tomtomtom1]

Hello @tomtomtom1
You need to do several problems to get a feel for it.

What you have to do is take the beam, do a cut in it, and then do a FBD ( free body diagram ) of the cut beam, determining the forces on the cut face.
Say you cut the beam 1.4 way from the left end.
There is a force of 5 kN in the y- direction at point 0.
What forces would have to act on the face to keep the cut beam in static equilibrium?

256bits

Thank you for the reply.

I have done a simple problem and created a SFD for it as shown below:-

I am trying to understand the SFD - if I was to cut the beam at 2m and evaluate the shear force on the left of the cut then I get a value of 12.5kN - is it correct to say that the shear force at my point is 12.5kN.

Also given the above SFD what is the max shear force - is it the largest positive value or largest negative value or the largest value regardless of sign?

Thank you.

 

[Chestermiller]

256bits

Thank you for the reply.

I have done a simple problem and created a SFD for it as shown below:-View attachment 252502

I am trying to understand the SFD - if I was to cut the beam at 2m and evaluate the shear force on the left of the cut then I get a value of 12.5kN - is it correct to say that the shear force at my point is 12.5kN.

Also given the above SFD what is the max shear force - is it the largest positive value or largest negative value or the largest value regardless of sign?

Thank you.

At the exact 2 meter location, the shear force is double valued, so, to be conservative, you would use the larger value. In terms of failure, the only thing that matters is the magnitude of the shear force, not its direction.

 

[256bits]

256bits

Thank you for the reply.

I have done a simple problem and created a SFD for it as shown below:-View attachment 252502

I am trying to understand the SFD - if I was to cut the beam at 2m and evaluate the shear force on the left of the cut then I get a value of 12.5kN - is it correct to say that the shear force at my point is 12.5kN.

Also given the above SFD what is the max shear force - is it the largest positive value or largest negative value or the largest value regardless of sign?

Thank you.

I think that diagram looks correct.

Well the change in sign is just a designation of the direction of the shear.
Magnitude of the shear would be the thing to look at.

 

[tomtomtom1]

I think that diagram looks correct.

Well the change in sign is just a designation of the direction of the shear.
Magnitude of the shear would be the thing to look at.

Thanks again 256bits

The bit now is the sign convention for Shear & Bending, for example:-

I have a simply supported beam for which I have calculated the reactions for.

I am interested in calculating the shear and moment at the dotted line.

For shear (v) is the convention to always make shear +ve as shown in red or -ve as shown in green.

For Bending (M) is the convention to always make Bending +ve as shown in yellow or -ve as shown in blue.

I am asking because how you set M or V i.e + or - will change the sign of the corresponding shear/moment.

Can you shed any light?

Thank you.

 

[256bits]

Can you shed any light?

In your green and red calculation fir shear, you have assumed a certain direction for the shear force. If the calculated shear is positive you have assumed correct. If the answer comes out negative, then the actual direction is opposite to your assumption .
You should be able to guide yourself for the calculation of the moment in the same way.

 

[256bits]

I may not be able to reply for a whole, so adjust accordingly.
Another member(s) of PF will be able to offer help.

 

[PhanthomJay]

I may not be able to reply for a whole, so adjust accordingly.
Another member(s) of PF will be able to offer help.

As 256bits has noted, be sure in your free body diagram and to show the correct direction of all the known Forces and moments. Then at the cut section, you can choose the up or down direction for the unknown shear, ,the left or right direction for unknown normal axial load, if present, and clockwise or counter clockwise for the unknown moment.

Then when you apply the equilibrium equations, if your answer for the unknowns in each case come out positive, you assumed the correct direction. and if your answer comes out negative, you have assumed the wrong direction, and you should immediately adjust your free body diagram to show the correct direction and magnitude.

Note that the direction does not necessarily indicate positive or negative shears or moments, because if you looked at the portion of the beam from the cut to the right side end of the beam, your directions are reversed due to Newton's 3rd law.. So rather than memorize for example that ccw moments on a left section are positive and ccw moments on a right section are negative, and get all mixed up, do not assign a plus or minus value to the shear and moment at this time.

Instead, draw the shear and moment diagrams, and shear values above the horizontal x-axis are positive, and below the axis are negative. Same with the moment diagrams, above the axis are positive (so-called sagging moments because the beam deflection (curvature) is concave at that particular point, tension stresses at the bottom of the beam) and below the x axis, the moments are negative (so called hogging moments with a convex curvature, tension stresses at the top of the beam).

In drawing the shear and moment diagrams, remember from the calculus that the slope of the moment diagram at a point along the beam is equal to the shear at that point. If the shear is positive, the moment diagram slope is positive(sloping upward).

So you can use either of your equilibrium equations you showed, just remember the negative result means you assumed the wrong direction.

It is most unfortunate that in determining the value of the moment at the cut section, you had a math error and got the wrong answer. That really confuses stuff. So check your math again.