Understanding Simultaneity Through Male & Female Clocks Meeting

[Master Wayne]

This is not a homework question, just a scenario I've come up with. Imagine I have a male and a female clock moving towards each other. If they're in sync, one will fit inside the other and they'll continue on their way. If not, they'll collide. (Apologies for the crude drawings.)

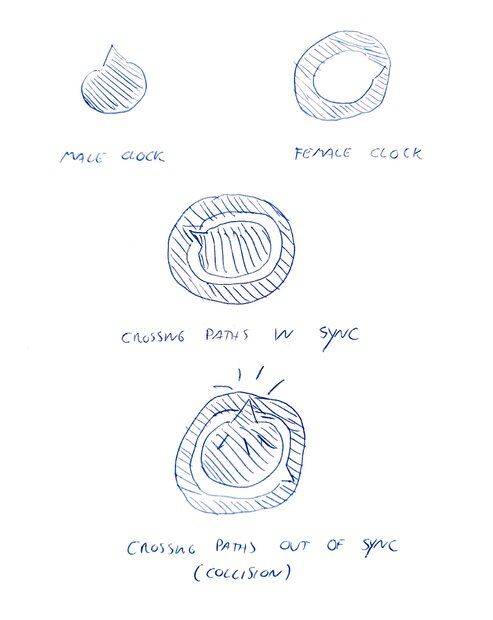
I place these clocks the same distance away from a midway point which contains a light bulb. The clocks travel toward the midway point at the same speed, meeting at that point some time later. Before the clocks start their journey, I set them to show time zero and turn them off. As soon as the clocks start, the light bulb emits a flash that travels in all directions. When that flash hits the clocks, they turn on and start keeping time.

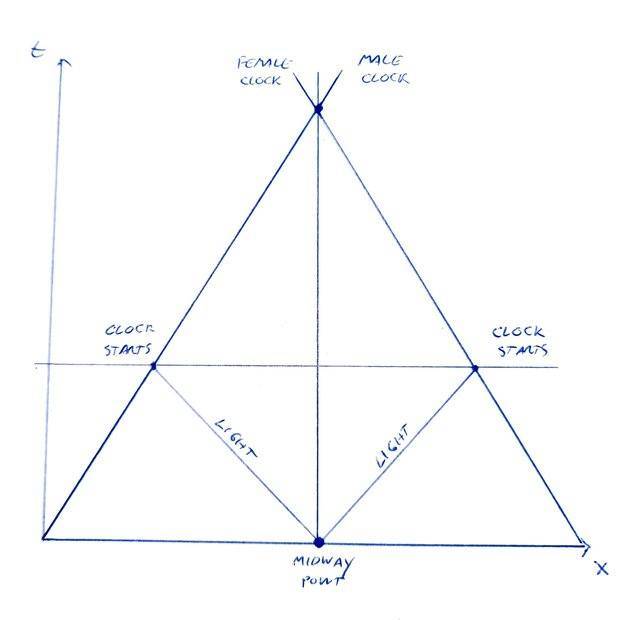
From a reference frame at rest with respect to the midway point, the clocks will always be in sync and when they meet at the midway point the male clock will pass through the female clock with no issue. Therefore, this is the outcome we must expect in all reference frames.

Now, let's analyze things from the reference frame of the male clock. In the image below, I've drawn the axes corresponding to that frame.

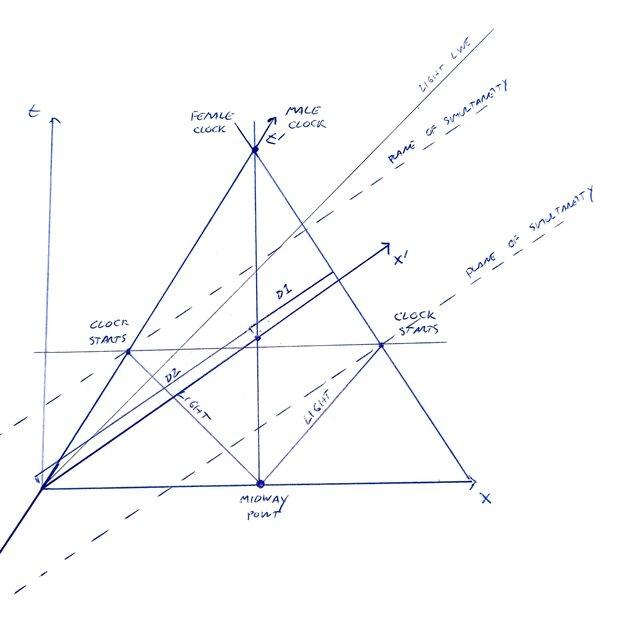
As we can see, from the male clock's frame the light flash starts the female clock first and only some time later starts the male clock. Therefore, the female clock gets a head start. However, from the male clock's frame the female clock also runs slow due to time dilation. To avoid a paradox, these two facts must combine in order to allow for a perfect synchronization of the clocks at the midway point.

What I'm having a hard time figuring out is how to make this analysis algebraic in order to demonstrate that this synchronization does happen from the male clock's frame. How can I show that from the male clock's frame, the female clock's head start is compensated by time dilation?

Bonus question (which is also confusing me): how come from the male clock's frame, at any given point in time, the distance D2 between the male clock and the midway point is larger than the distance D1 between the midway point and the female clock? Shouldn't I expect both distances to contract equally? This is the difficulty which has prevented me from drawing a new spacetime diagram from the perspective of the male clock (I can't figure out why the initial conditions would be spatially asymmetric).

 

[Orodruin]

How can I show that from the male clock's frame, the female clock's head start is compensated by time dilation?

Just compute the proper time of the male and female clocks from being started to when they meet.

 

[Nugatory]

How can I show that from the male clock's frame, the female clock's head start is compensated by time dilation?

You don’t, because you lose the effects of relativity of simultaneity - the conditions under which the time dilation and length contraction formulas can be applied are fairly restrictive, and this situation isn’t one in which those conditions hold.

Instead, write down the coordinates of all the relevant events using one frame (preferably the one in which the center is at rest - it ‘s easiest) and then use the full Lorentz transforms to find the coordinates in the frame in which the male clock is at rest.

 

[Orodruin]

Bonus question (which is also confusing me): how come from the male clock's frame, at any given point in time, the distance D2 between the male clock and the midway point is larger than the distance D1 between the midway point and the female clock?

Correct.

Shouldn't I expect both distances to contract equally?

No, you cannot apply length contraction in the way you seem to want to. One must be very careful about using the time dilation and length contraction formulas because they both come with a set of assumptions that are often glossed over in a way that makes them feel unimportant when they are in fact crucial.

 

[Ibix]

What I'm having a hard time figuring out is how to make this analysis algebraic in order to demonstrate that this synchronization does happen from the male clock's frame. How can I show that from the male clock's frame, the female clock's head start is compensated by time dilation?

Write down the $(t,x)$ coordinates of the various events in the symmetric frame, then use the Lorentz transforms to get the coordinates in any other frame. The Lorentz transforms preserve straight lines, so you only need the "junction" events.

This is also the answer to your bonus question.

 

[Sagittarius A-Star]

Shouldn't I expect both distances to contract equally?

No. The "length contraction" applies to a distance, which is constant over time in each frame.

 

[Master Wayne]

Just compute the proper time of the male and female clocks from being started to when they meet.

I followed this suggestion and obtained the expected result. Thanks for the suggestions. I will now try to do the same using the Lorentz transformations.

 

[Master Wayne]

Correct.No, you cannot apply length contraction in the way you seem to want to. One must be very careful about using the time dilation and length contraction formulas because they both come with a set of assumptions that are often glossed over in a way that makes them feel unimportant when they are in fact crucial.

Follow-up question: when setting up the problem from the male clock's frame, I'd expect the midway point to move towards the male clock with speed $v$, and the female clock to move towards the male clock with speed $2v$. However, since $D1$ and $D2$ are different ($D2 > D1$) at all times, the ratio between the female clock's speed and the male clock's speed is not 2, but a smaller number. I'm having trouble understanding if this result is correct and if so, why?

 

[PeroK]

Follow-up question: when setting up the problem from the male clock's frame, I'd expect the midway point to move towards the male clock with speed $v$, and the female clock to move towards the male clock with speed $2v$. However, since $D1$ and $D2$ are different ($D2 > D1$) at all times, the ratio between the female clock's speed and the male clock's speed is not 2, but a smaller number. I'm having trouble understanding if this result is correct and if so, why?

Look up relativistic velocity addition. It can't be $2v$ as then the relative velocity would be $> c$ when $v> \frac c 2$.

 

[Master Wayne]

Look up relativistic velocity addition. It can't be $2v$ as then the relative velocity would be $> c$ when $v> \frac c 2$.

Of course, makes perfect sense.

But what if I'm trying to setup this same problem from the start from the reference frame of the male clock? Would I be wrong in drawing a spacetime diagram where the female clock's worldline starts at $x' = 2d$, the midpoint's worldline starts at $x' = d$ and both intersect the $t'$ axis at the same point? After all, this would imply that the female clock's speed is indeed $2v$ (where $v$ is the midpoint's speed), and that $D1$ and $D2$ start out equal to each other. But these are not the results we have found in this discussion so far. Seems odd that I would have to take into consideration the results from another frame of reference when setting up the initial conditions for this frame of reference. What am I missing?

 

[PeroK]

What am I missing?

The full Lorentz Transformation. Think coordinates.

 

[PeterDonis]

what if I'm trying to setup this same problem from the start from the reference frame of the male clock?

Do you mean truly set up the same problem? Or a different problem?

The same problem means all of the events have the same geometric relationship. That means all observables will be the same. It also means the coordinates you use to set up the events in the male clock's frame will not be the same as the ones you used in your OP.

If you use the same coordinates, but now in the male clock's frame instead of the frame you used in your OP, you are setting up a different problem: the geometric relationships between the events will be different. So you should expect different results.

 

[Master Wayne]

Do you mean truly set up the same problem? Or a different problem?

The same problem means all of the events have the same geometric relationship. That means all observables will be the same. It also means the coordinates you use to set up the events in the male clock's frame will not be the same as the ones you used in your OP.

If you use the same coordinates, but now in the male clock's frame instead of the frame you used in your OP, you are setting up a different problem: the geometric relationships between the events will be different. So you should expect different results.

Makes perfect sense. Thank you very much.