- #1
Understanding Taylor Series Approximation with Taylor's Theorem Explanation
- Thread starter rmc240
- Start date
-
- Tags
- Series Taylor Taylor series
In summary, the conversation discusses the use of an approximation in a derivation, specifically how Taylor's theorem allows for this approximation. The participants also touch on recognizing and evaluating the function at a certain point.
- #2
- 9,568
- 775
rmc240 said:I'm reading a derivation and it says that the following approximation can be used:
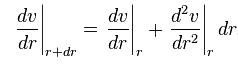
I do not under stand how Taylor's theorem allows for this approximation. Can anyone explain this a little?
If you let ##f(r) = \frac{dv}{dr}## you have ##f(r+dr) = f(r) + f'(r)dr##. Do you recognize that?
- #3
rmc240
- 4
- 0
Yea, my problem was realizing that I was supposed to approximate the function around r and evaluate the function at r + dr. Should have seen that. Thank you for your help.
FAQ: Understanding Taylor Series Approximation with Taylor's Theorem Explanation
What is a Taylor series?
A Taylor series is a mathematical representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point.
Why are Taylor series useful?
Taylor series are useful because they allow us to approximate a complex function with a simpler polynomial function, which can then be used to approximate the values of the original function at any point.
How do you find the Taylor series of a function?
To find the Taylor series of a function, you need to calculate the derivatives of the function at a single point and then plug those values into the general Taylor series formula. The more derivatives you calculate, the more accurate the approximation will be.
What is the difference between a Taylor series and a Maclaurin series?
A Maclaurin series is a specific type of Taylor series where the point of expansion is at x=0. This means that all the derivatives used in the Maclaurin series are evaluated at x=0, making it a more simplified version of the general Taylor series.
What are some applications of Taylor series?
Taylor series are used in many areas of mathematics and science, including physics, engineering, and finance. They are especially useful in approximating functions that are difficult to integrate or differentiate, and in solving differential equations.