paulimerci
- 287
- 47
- Homework Statement
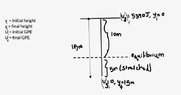
- Find the total energy of a 55kg bungee jumper who jumps off a bridge and comes to rest 10m above the water while the bungee with a spring constant of 25N/m is stretched 15m.
- Relevant Equations
- Total energy = 1/2 kx^2 + mgh
There is a three-step energy transformation. Gravitational potential energy(GPE) is stored energy associated with an object's height above the ground. So here, the bungee jumper who is on a bridge 10m above the water has GPE. As the jumper jumps off the bridge, this stored energy is converted into K.E soon this energy will begin to be transformed into Elastic potential energy as the bungee cord is flexed to its maximum extent.
Given values are m = 55kg , h = 10m, ##k = 25 \frac {N}{m}##, stretched distance = 15m, displacement (x) = stretched distance - unstretched distance = 15-10m
The total energy of the system, TE, is the sum of all the different energies present in the system:
TE = Elastic PE + mgh
$$ TE = \frac {1}{2} kx^2 + mgh$$
$$ TE = \frac {1}{2} 25 \cdot 5^2 + 55 \cdot 9.8 \cdot 10$$
$$ TE = 5702J$$
Have I done it right?
Given values are m = 55kg , h = 10m, ##k = 25 \frac {N}{m}##, stretched distance = 15m, displacement (x) = stretched distance - unstretched distance = 15-10m
The total energy of the system, TE, is the sum of all the different energies present in the system:
TE = Elastic PE + mgh
$$ TE = \frac {1}{2} kx^2 + mgh$$
$$ TE = \frac {1}{2} 25 \cdot 5^2 + 55 \cdot 9.8 \cdot 10$$
$$ TE = 5702J$$
Have I done it right?