- #1
Spacepantz86
- 5
- 1
I do not understand the principle, to me it would make more sense if there was no line, there is nothing.
The best way I can think of it would be, the first dimension is the observer, or nothing.
I really don't know, its just this way makes more sense in my head, though I am lacking any knowledge of physics really.
Sorry about my ignorance, just wanting to learn :)
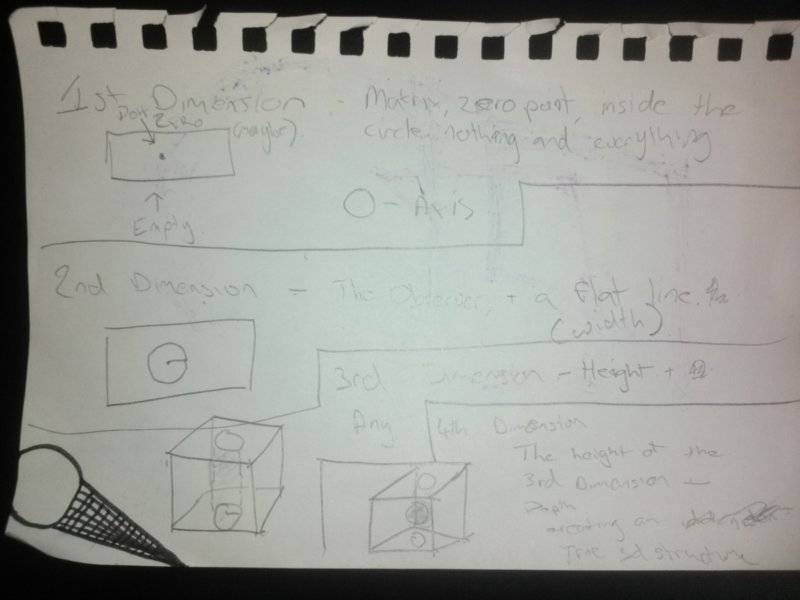
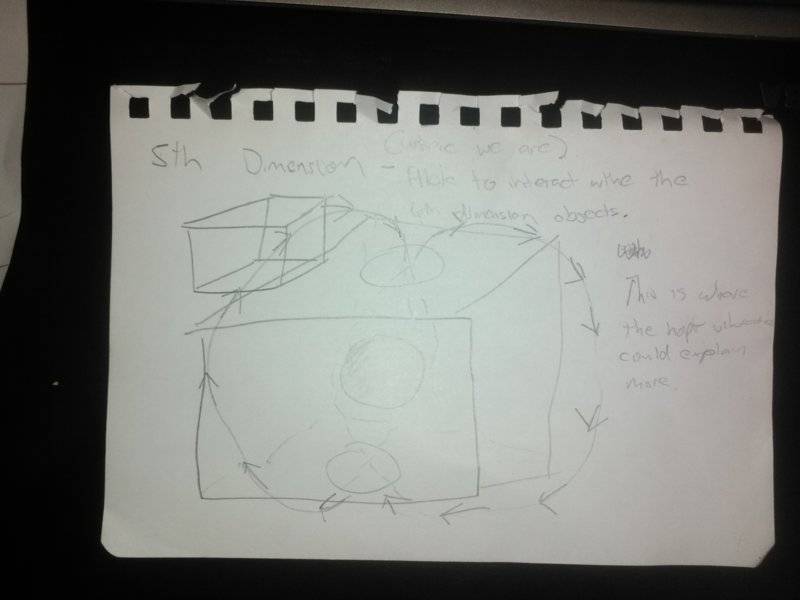
The best way I can think of it would be, the first dimension is the observer, or nothing.
I really don't know, its just this way makes more sense in my head, though I am lacking any knowledge of physics really.
Sorry about my ignorance, just wanting to learn :)

